Logical Error Rates of XZZX and Rotated Quantum Surface Codes
2024-09-02 21:26
2894 浏览
Source:IEEE Journal on Selected Areas in Communications ( Volume: 42, Issue: 7, July 2024) DOI:10.1109/JSAC.2024.3380088
Abstract
Surface codes are versatile quantum error-correcting codes known for their planar geometry, making them ideal for practical implementations. While the original proposal used Pauli X or Pauli Z operators in a square structure, these codes can be improved by rotating the lattice or incorporating a mix of generators in the XZZX variant. However, a comprehensive theoretical analysis of the logical error rate for these variants has been lacking. To address this gap, we present theoretical formulas based on recent advancements in understanding the weight distribution of stabilizer codes. For example, over an asymmetric channel with asymmetry A=10 and a physical error rate p→0 , we observe that the logical error rate asymptotically approaches pL→10 p2 for the rotated [[9,1,3]] XZZX code and pL→18.3 p2 for the [[13,1,3]] surface code. Additionally, we observe a particular behavior regarding rectangular lattices in the presence of asymmetric channels. Our findings demonstrate that implementing both rotation and XZZX modifications simultaneously can lead to suboptimal performance. Thus, in scenarios involving a rectangular lattice, it is advisable to avoid using both modifications simultaneously.

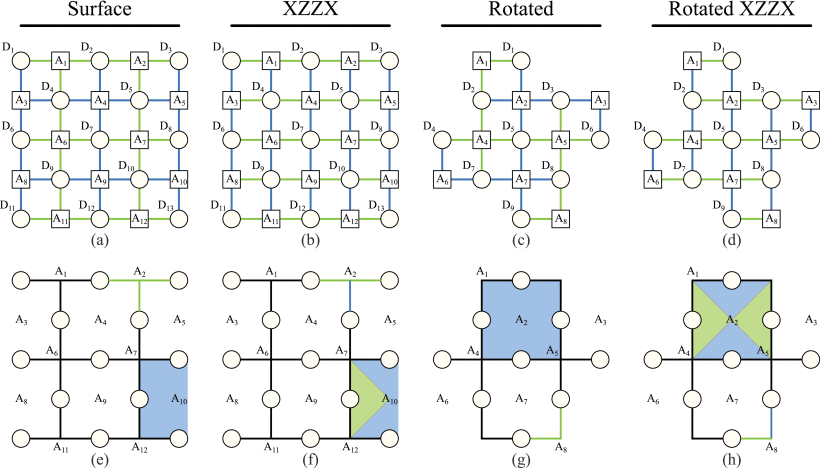
(a, e) [[13,1,3]] surface code, (b, f) [[13,1,3]] XZZX code, (c, g) [[9,1,3]] rotated surface code, (d, h) [[9,1,3]] rotated XZZX code. The first row represent the actual code structure with data qubits (circles) and ancillas (squares). Z measurements are depicted in blue, while X measurements are depicted in green. The second row is a simplified representation of the lattice with sites and plaquettes.
