Comprehensive explanation of ZZ coupling in superconducting qubits
2024-08-29 19:58
2993 浏览Abstract: A major challenge for scaling up superconducting quantum computers is unwanted couplings between qubits, which lead to always-on ZZ couplings that impact gate fidelities by shifting energy levels conditional on qubit states. To tackle this challenge, we introduce analytical and numerical techniques, including a diagrammatic perturbation theory and a state-assignment algorithm, as well as a refined intuitive picture for the workings of the ZZ coupling. Together, these tools enable a deeper understanding of the mechanisms behind the ZZ coupling and facilitate finding parameter regions of weak and strong ZZ coupling. We showcase these techniques for a system consisting of two fixed-frequency transmon qubits connected by a flux-tunable transmon coupler. There, we find three types of parameter regions with zero or near-zero ZZ coupling, all of which are accessible with current technology. We furthermore find regions of strong ZZ coupling nearby, which may be used to implement adiabatic controlled-phase gates. Our methods are applicable to many types of qubits and open up for the design of large-scale quantum computers with improved gate fidelities.
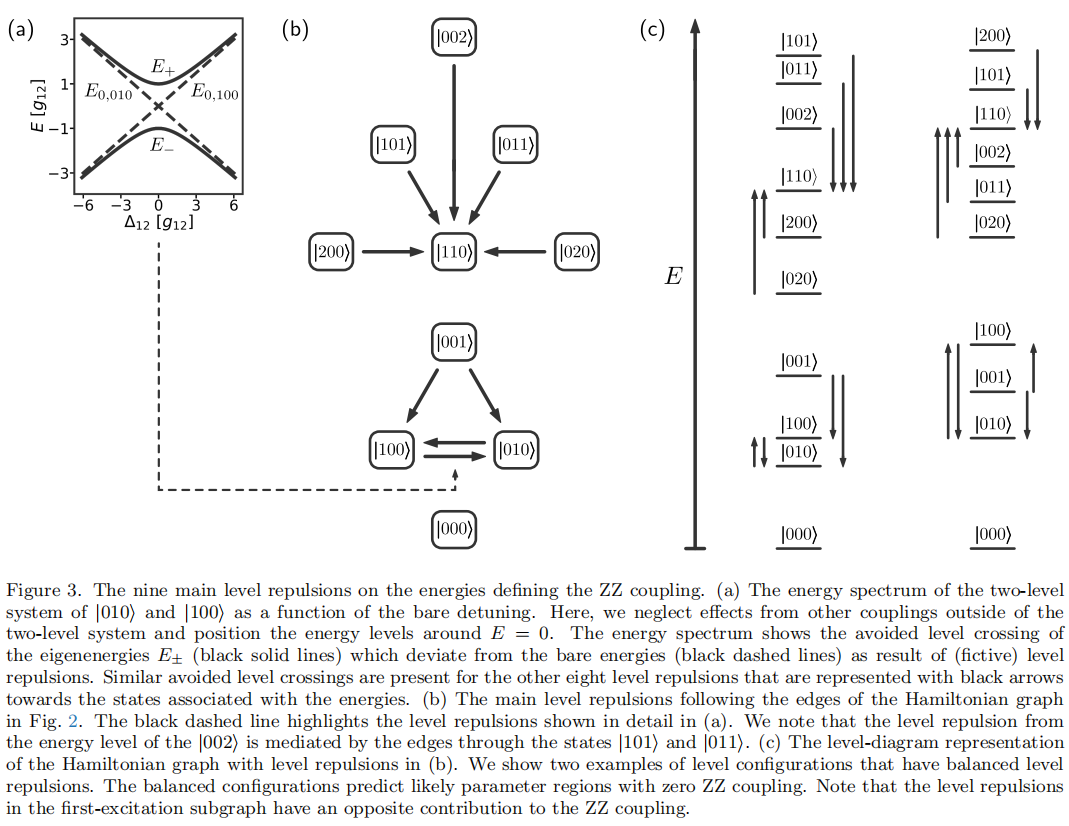
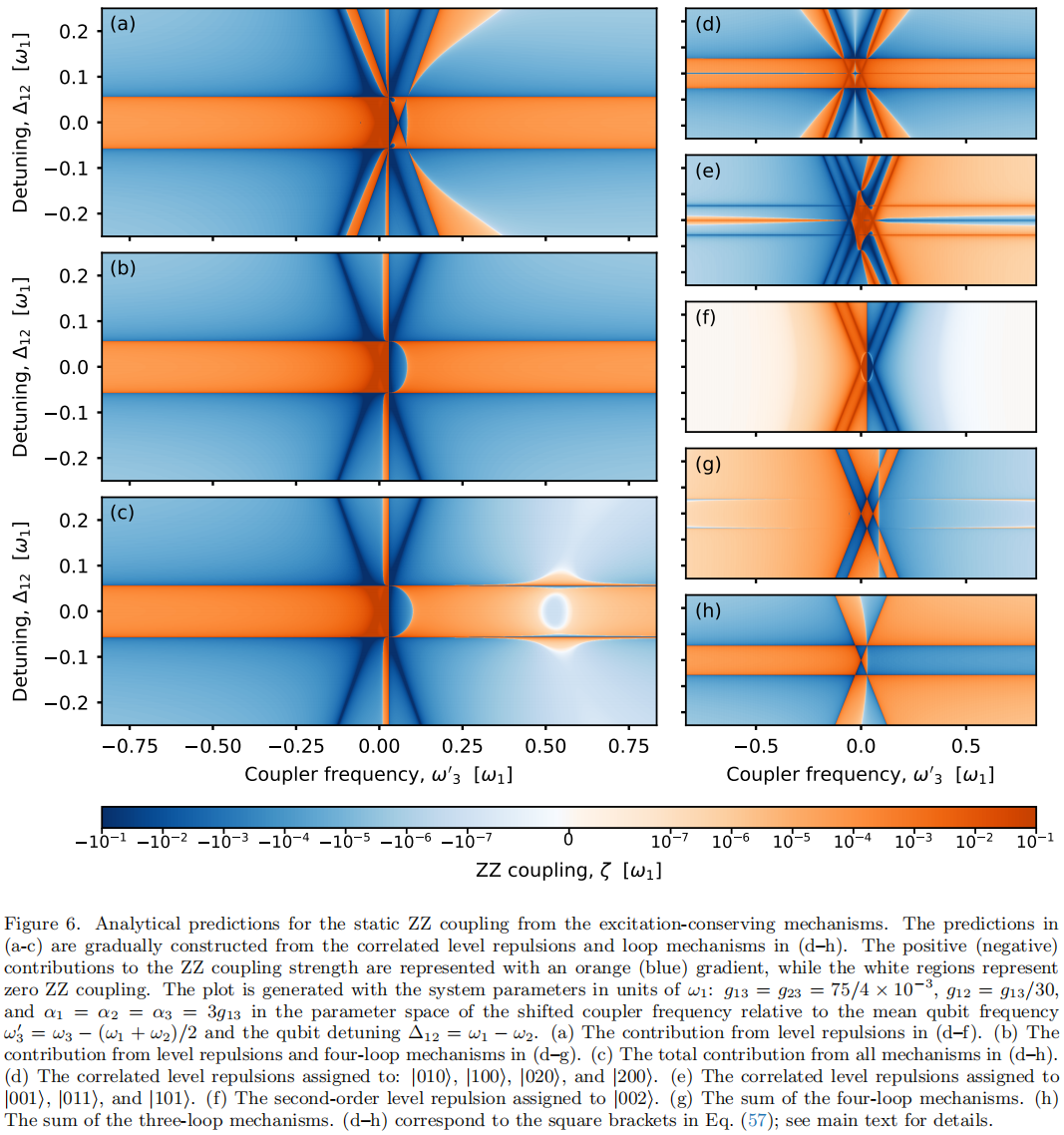
Conclusion: We have introduced improved analytical and numerical methods to understand and calculate the ZZ coupling between qubits.Through these methods, we have shown how to find parameter regions with weak and strong ZZ coupling for two fixed-frequency superconducting transmon qubits connected by a flux-tunable coupler qubit. Regions with weak ZZ coupling enable the operation of high-fidelity quantum gates and algorithms by eliminating a type ofcoherent error pervasive in quantum computers, while regions with strong ZZ coupling can be harnessed for implementing fast (and thus high-fidelity) CPHASE or CZ gates. Our improvement of analytical methods for handling ZZ coupling consists of a diagrammatic formalism for perturbation theory using the Schrieffer-Wolff transformation. This formalism is closely connected to a graph representation of the Hamiltonian for the system. The diagrams in the formalism enable efficient bookkeeping of the many terms at higher perturbative orders, but also greatly enhance our understanding of the mechanisms for the ZZ coupling by showing which processes contribute to it.
