Simulation and performance analysis of quantum error correction with a rotated surface code under a realistic noise model

2024-09-05 14:49　77 浏览

Source

DOI:https://doi.org/10.1103/PhysRevResearch.6.013024

ABSTRACT

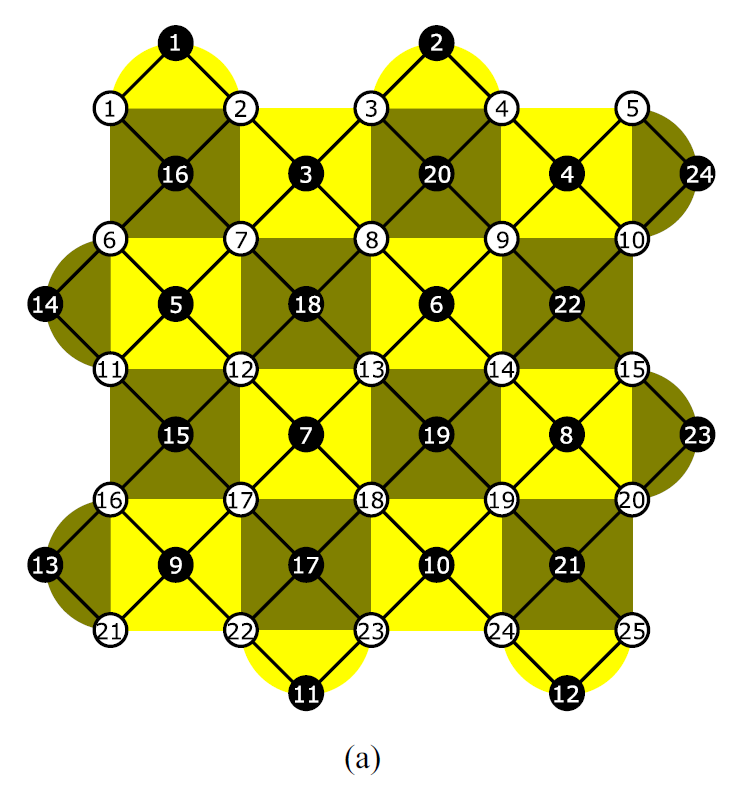
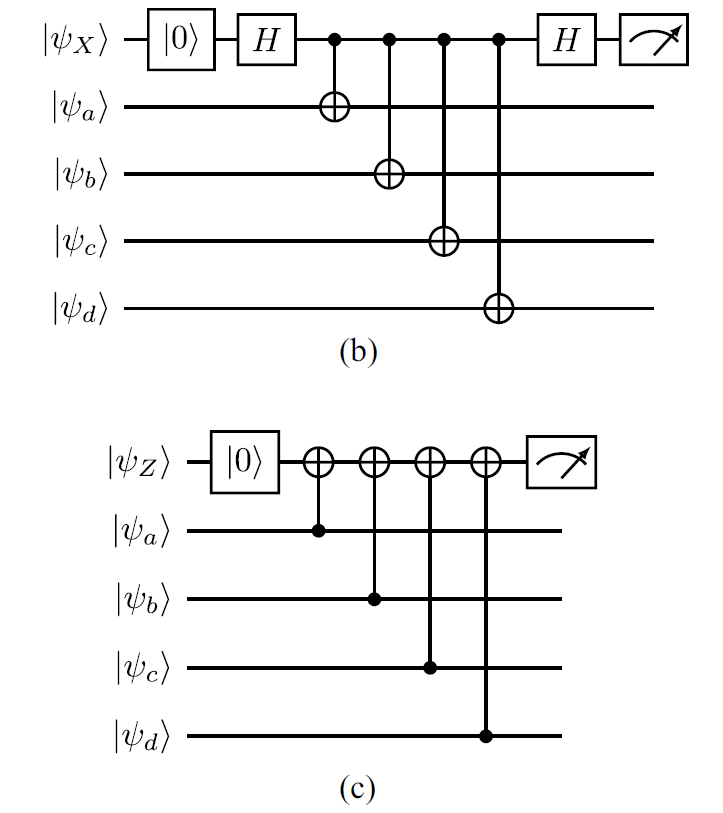
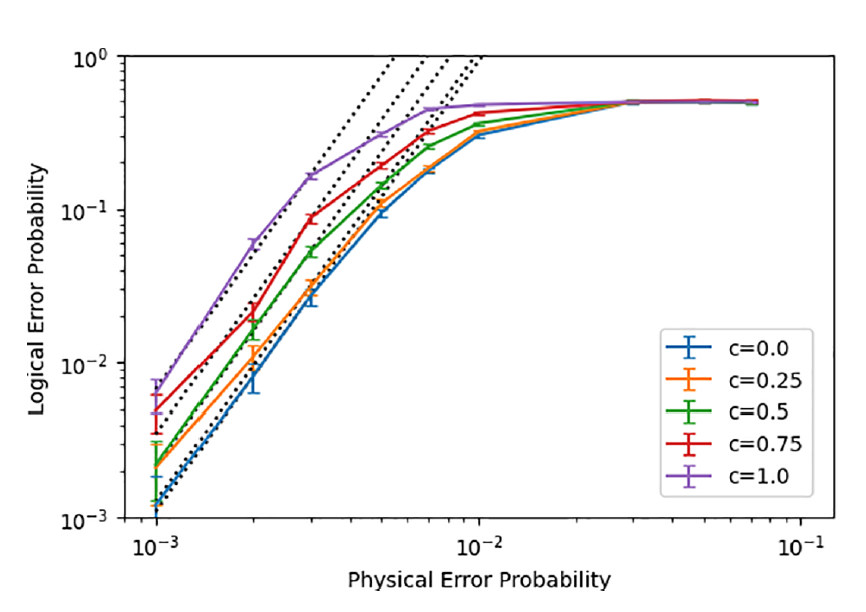
The demonstration of quantum error correction (QEC) is one of the most important milestones in the realization of fully-fledged quantum computers. Toward this, QEC experiments using the surface codes have recently been actively conducted. However, it has not yet been realized to protect logical quantum information beyond the physical coherence time. In this work, we performed a full simulation of QEC for the rotated surface codes with a code distance 5, which employs 49 qubits and is within reach of the current state-of-the-art quantum computers. In particular, we evaluate the logical error probability in a realistic noise model that incorporates not only stochastic Pauli errors but also coherent errors due to a systematic control error or unintended interactions. While a straightforward simulation of 49 qubits is not tractable within a reasonable computational time, we reduced the number of qubits required to 26 qubits by delaying the syndrome measurement in simulation. This and a fast quantum computer simulator, qulacs, implemented on GPU allows us to simulate full QEC with an arbitrary local noise within reasonable simulation time. Based on the numerical results, we also construct and verify an effective model to incorporate the effect of the coherent error into a stochastic noise model. This allows us to understand what the effect coherent error has on the logical error probability on a large scale without full simulation based on the detailed full simulation of a small scale. The present simulation framework and effective model, which can handle arbitrary local noise, will play a vital role in clarifying the physical parameters that future experimental QEC should target.

CONCLUSION

In this study, we constructed a framework to fully simulate QEC on the distance 5 rotated surface code under an arbitrary local noise. Furthermore, we have constructed an effective model that explains the behavior of the logical error probability under the coherent errors within the stochastic Pauli noise model with an appropriate modification. Therefore, combining our numerical result and the effective model, we can analyze the behavior of the logical error probability with smaller a physical error probability or larger code distance. While we only modelled the over-rotation with fixed angle caused by a systematic control error, there are plenty of sources of coherent errors need to be taken account into such as unintended interactions in Hamiltonian, cross-talk, global fields, time-correlated coherent rotation and so on. These sources of noise would be straightforwardly incorporated into our framework. The performance analysis under more realistic noise models is becoming increasingly important, and our framework will provide a vital guideline for future improvements on experimental sides.