A General Framework for Gradient-Based Optimization of Superconducting Quantum Circuits using Qubit Discovery as a Case Study
2024-08-26 23:41
2866 浏览Abstract: Engineering the Hamiltonian of a quantum system is fundamental to the design of quantum systems. Automating Hamiltonian design through gradient-based optimization can dramatically accelerate this process. However, computing the gradients of eigenvalues and eigenvectors of a Hamiltonian—a large, sparse matrix—relative to system properties poses a significant challenge, especially for arbitrary systems. Superconducting quantum circuits offer substantial flexibility in Hamiltonian design, making them an ideal platform for this task. In this work,we present a comprehensive framework for the gradient-based optimization of superconducting quantum circuits, leveraging the SQcircuit software package. By addressing the challenge of calculating the gradient of the eigensystem for large, sparse Hamiltonians and integrating automatic differentiation within SQcircuit, our framework enables efficient and precise computation of gradients for various circuit properties or custom-defined metrics, streamlining the optimization process. We apply this framework to the qubit discovery problem, demonstrating its effectiveness in identifying qubit designs with superior performance metrics. The optimized circuits show improvements in a heuristic measure of gate count, upper bounds on gate speed, decoherence time, and resilience to noise and fabrication errors compared to existing qubits. While this methodology is showcased through qubit optimization and discovery, it is versatile and can be extended to tackle other optimization challenges in superconducting quantum hardware design.
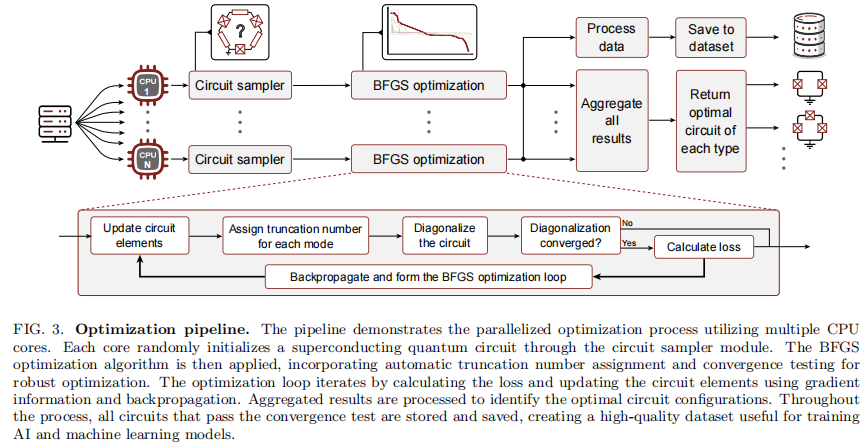
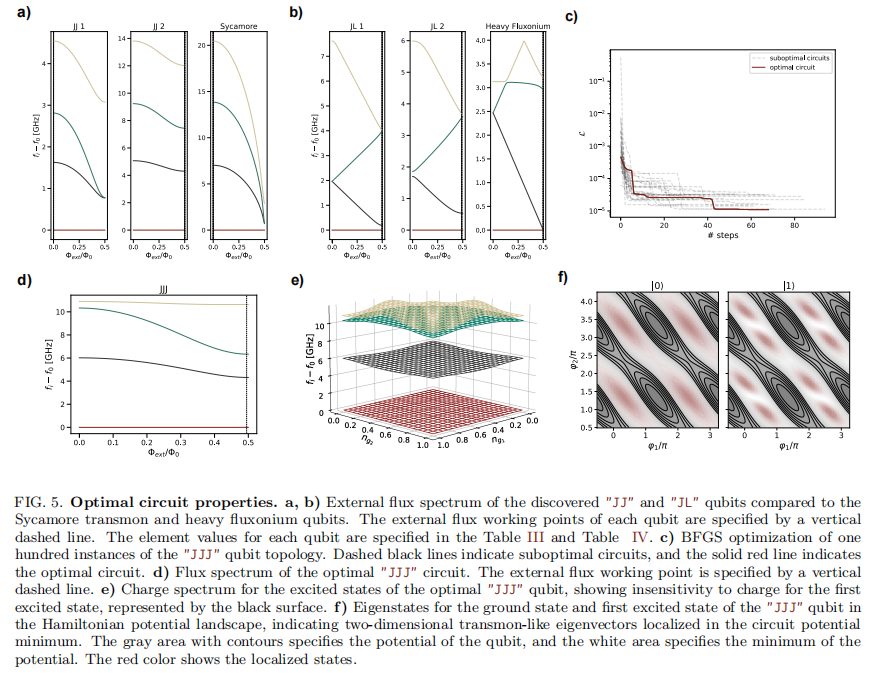
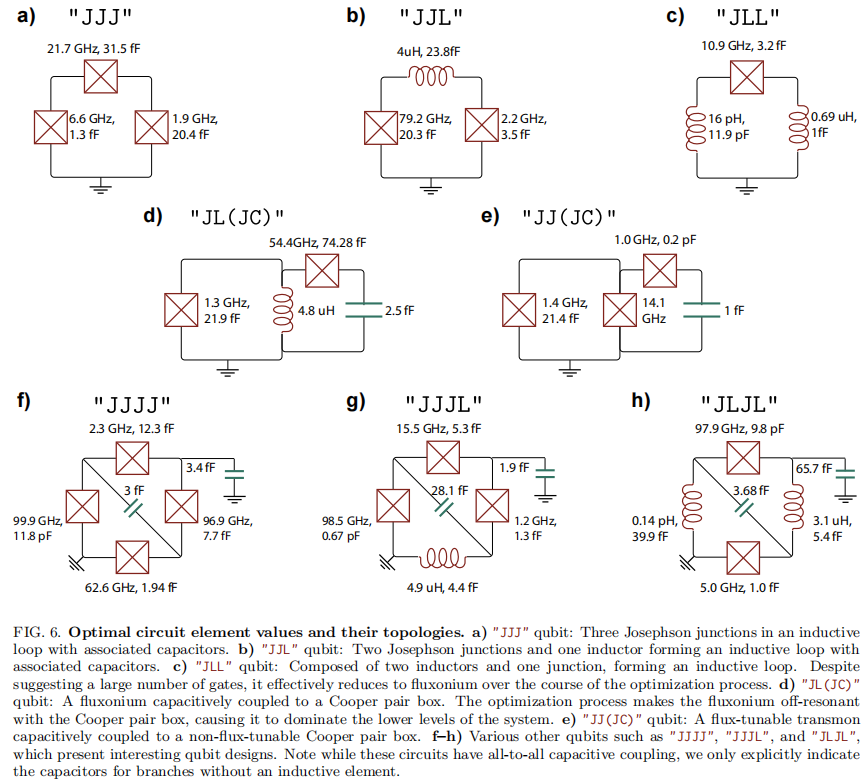
Conclusion: In this paper, we introduced a generalized framework for gradient-based optimization of superconducting quantum circuits using the SQcircuit software package. This framework incorporates automatic differentiation, enabling the efficient computation of gradients for various circuit properties with respect to arbitrary circuit elements. We demonstrated this approach by applying it to the qubit discovery problem,allowing for the identification of qubit designs with improved performance metrics. The methodology presented in this work is not limited to qubit discovery but can be extended to other optimization problems within the realm of superconducting quantum hardware. By leveraging the capabilities of SQcircuit, researchers can explore a wide range of circuit configurations and optimization criteria, ultimately accelerating the development of advanced quantum technologies.
