Diagonalization of large many-body Hamiltonians on a quantum processor

The estimation of low energies of many-body systems is a cornerstone of computational quantum sciences. Variational quantum algorithms can be used to prepare ground states on pre-fault-tolerant quantum processors, but their lack of convergence guarantees and impractical number of cost function estimations prevent systematic scaling of experiments to large systems. Alternatives to variational approaches are needed for large-scale experiments on pre-fault-tolerant devices. Here, we use a superconducting quantum processor to compute eigenenergies of quantum many-body systems on two-dimensional lattices of up to 56 sites, using the Krylov quantum diagonalization algorithm, an analog of the well-known classical diagonalization technique. We construct subspaces of the many-body Hilbert space using Trotterized unitary evolutions executed on the quantum processor, and classically diagonalize many-body interacting Hamiltonians within those subspaces. These experiments show that quantum diagonalization algorithms are poised to complement their classical counterpart at the foundation of computational methods for quantum systems.

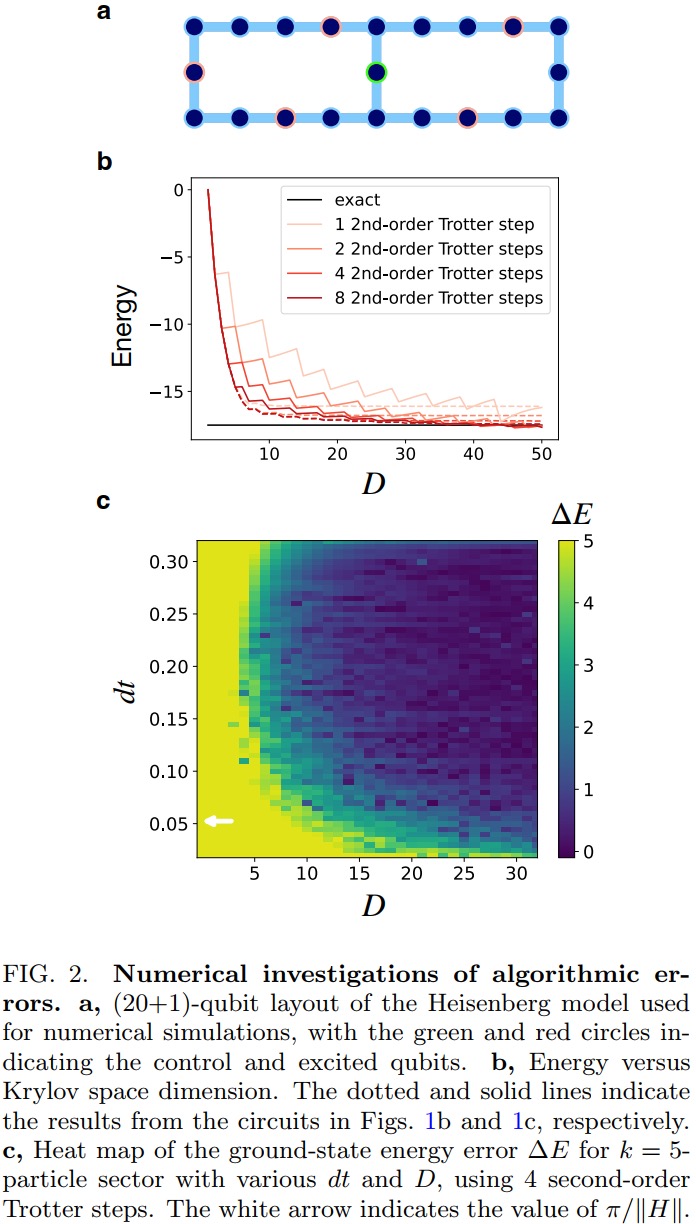
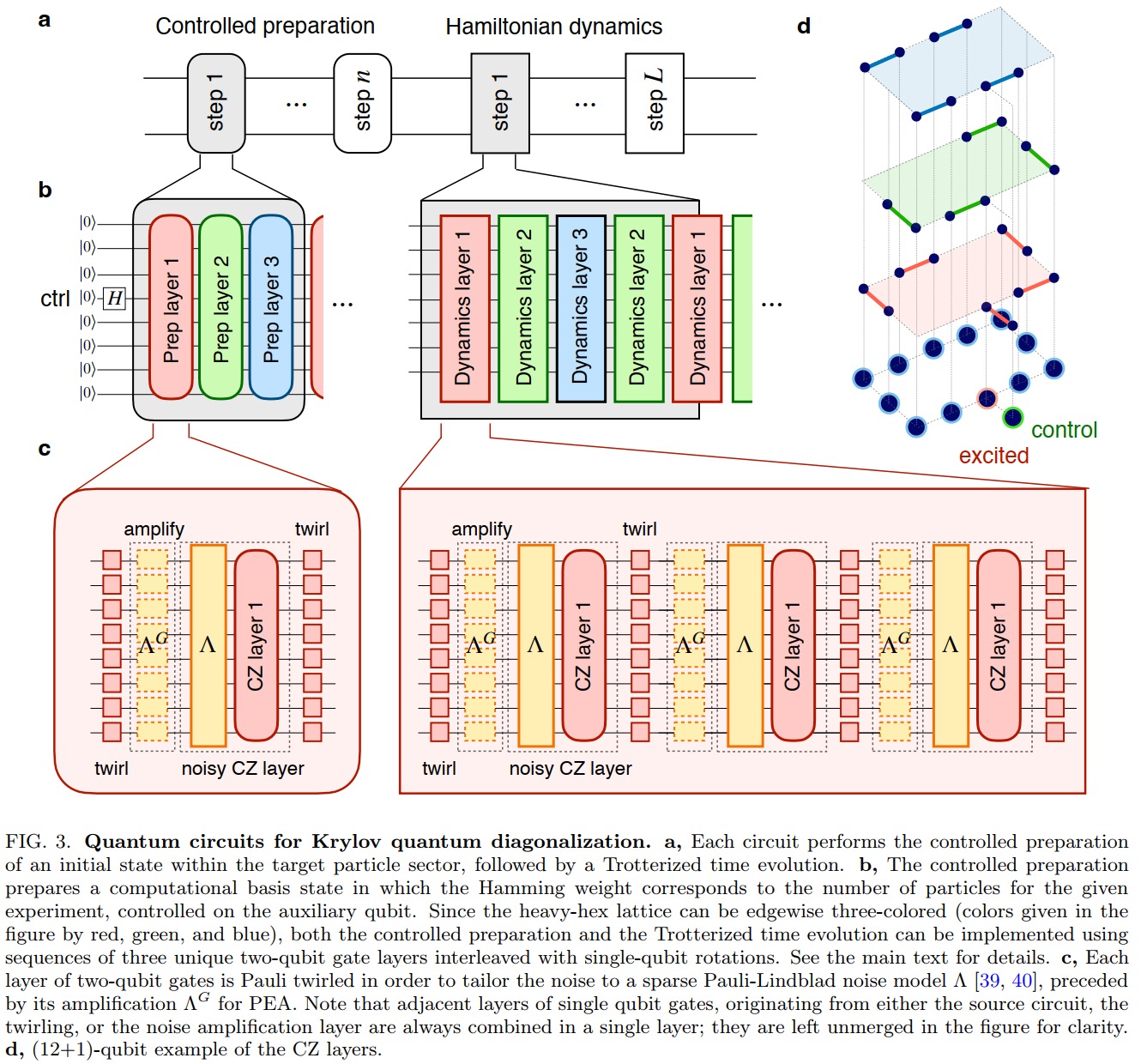
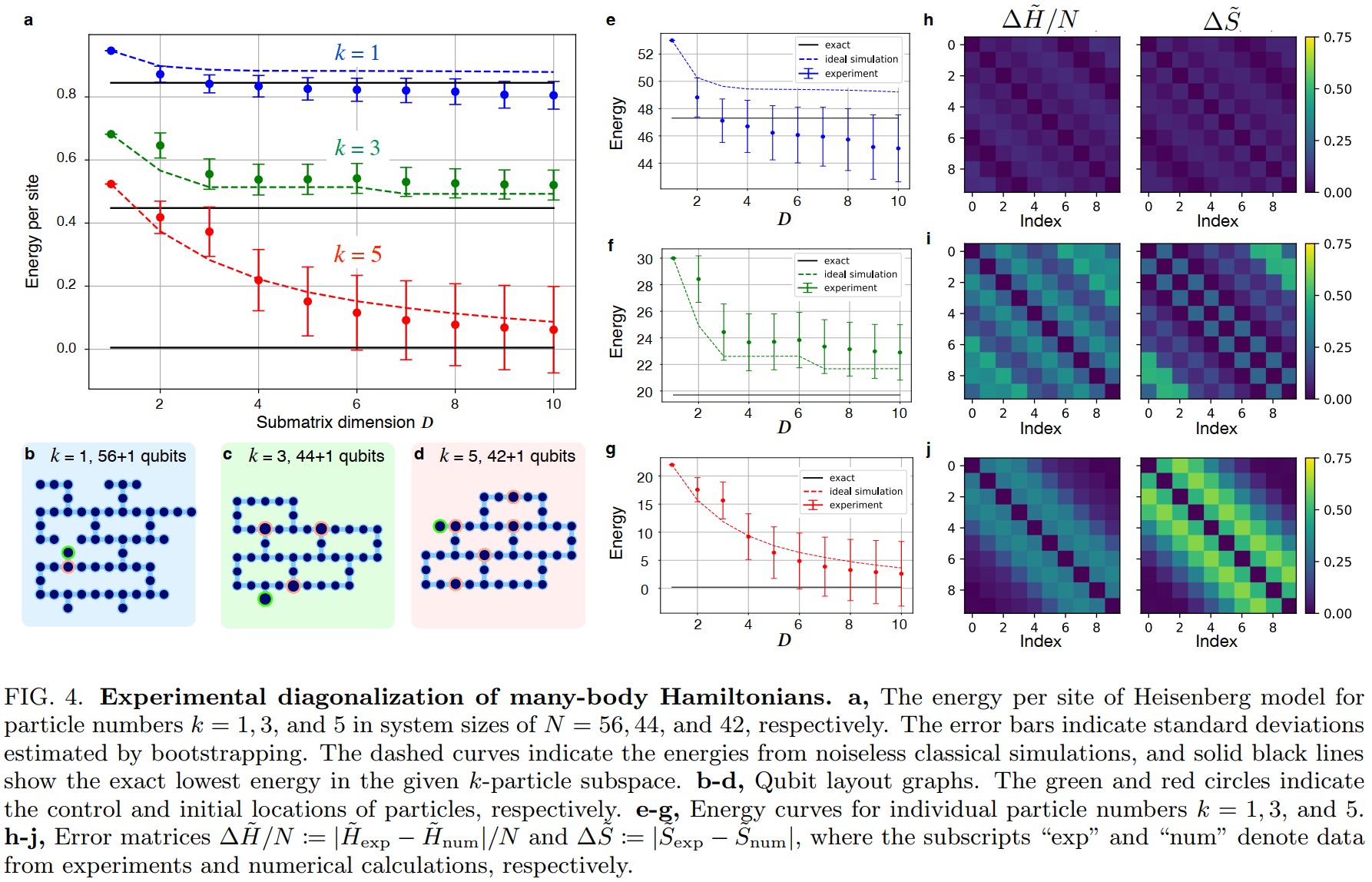
https://arxiv.org/pdf/2407.14431