Diagnostics of Mixed-State Topological Order and Breakdown of Quantum Memory
2024-05-29 09:18
1342 浏览
Topological quantum memory can protect information against local errors up to finite error thresholds. Such thresholds are usually
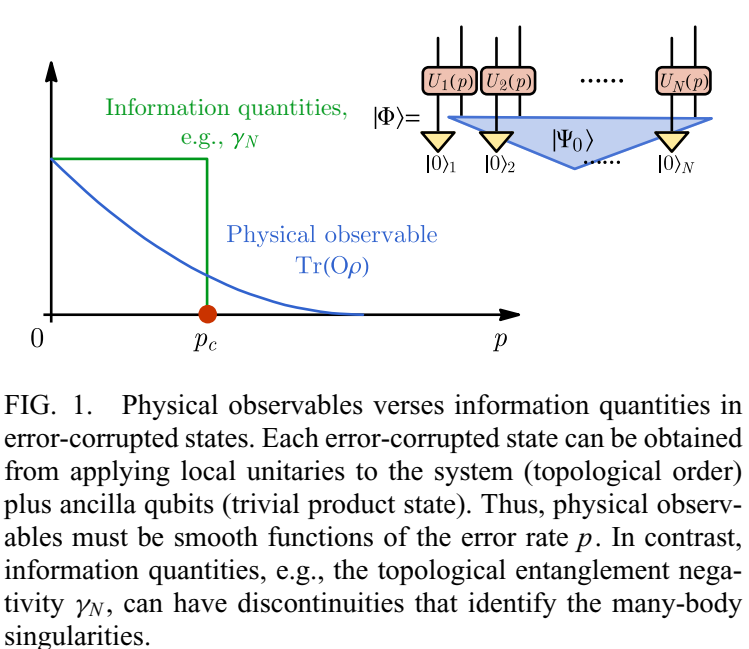
determined based on the success of decoding algorithms rather than the intrinsic properties of the mixed states describing corrupted
memories. Here we provide an intrinsic characterization of the breakdown of topological quantum memory, which both gives a bound on the
performance of decoding algorithms and provides examples of topologically distinct mixed states. We employ three information-theoretical
quantities that can be regarded as generalizations of the diagnostics of ground-state topological order, and serve as a definition for
topological order in error-corrupted mixed states. We consider the topological contribution to entanglement negativity and two other metrics
based on quantum relative entropy and coherent information. In the concrete example of the two-dimensional (2D) Toric code with local
bit-flip and phase errors, we map three quantities to observables in 2D classical spin models and analytically show they all undergo a
transition at the same error threshold. This threshold is an upper bound on that achieved in any decoding algorithm and is indeed saturated
by that in the optimal decoding algorithm for the Toric code.

Article: https://doi.org/10.1103/PRXQuantum.5.020343
