Quantum Simulation of the Tricritical Ising Model in Tunable Josephson Junction Ladders
2024-05-29 09:01
1381 浏览 Modern hybrid superconductor-semiconductor Josephson junction arrays are a promising platform for analog quantum
simulations. Their controllable and nonsinusoidal energy-phase relation opens the path to implement nontrivial interactions and study
the emergence of exotic quantum phase transitions. Here, we propose the analysis of an array of hybrid Josephson junctions defining
a two-leg ladder geometry for the quantum simulation of the tricritical Ising phase transition. This transition provides the paradigmatic
example of minimal conformal models beyond Ising criticality and its excitations are intimately related to Fibonacci non-Abelian
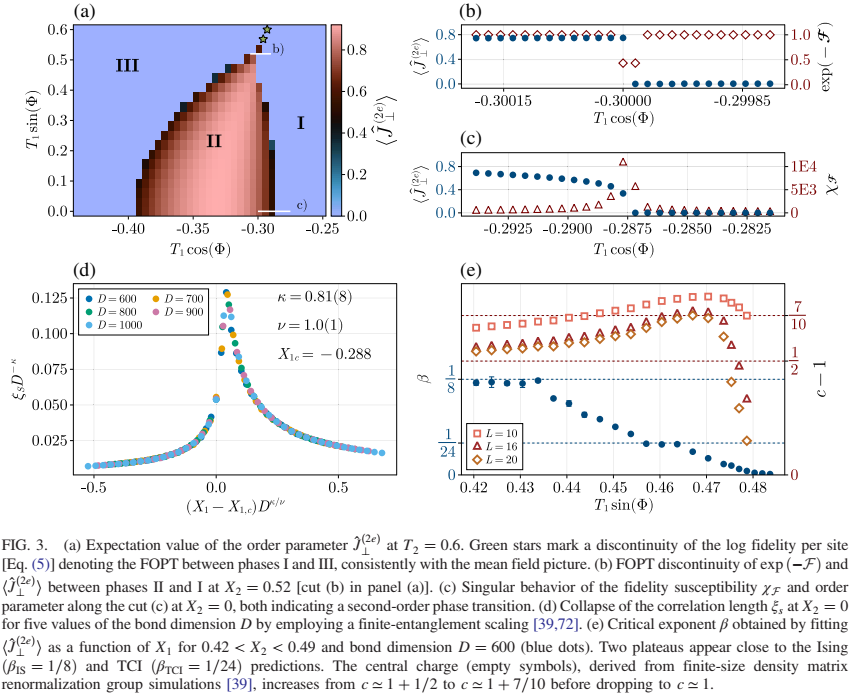
anyons and topological order in two dimensions. We study this superconducting system and its thermodynamic phases based on
bosonization and matrix-product-state techniques. Its effective continuous description in terms of a three-frequency sine-Gordon
quantum field theory suggests the presence of the targeted tricritical point and the numerical simulations confirm this picture. Our
results indicate which experimental observables can be adopted in realistic devices to probe the physics and the phase transitions of
the model. Additionally, our proposal provides a useful one-dimensional building block to design exotic topological order in two-
dimensional scalable Josephson junction arrays.
Article: https://doi.org/10.1103/PhysRevLett.132.226502
