Phase-Sensitive Quantum Measurement without Controlled Operations
2024-05-29 08:59
1310 浏览
Many quantum algorithms rely on the measurement of complex quantum amplitudes. Standard approaches to obtain the phase information, such as the
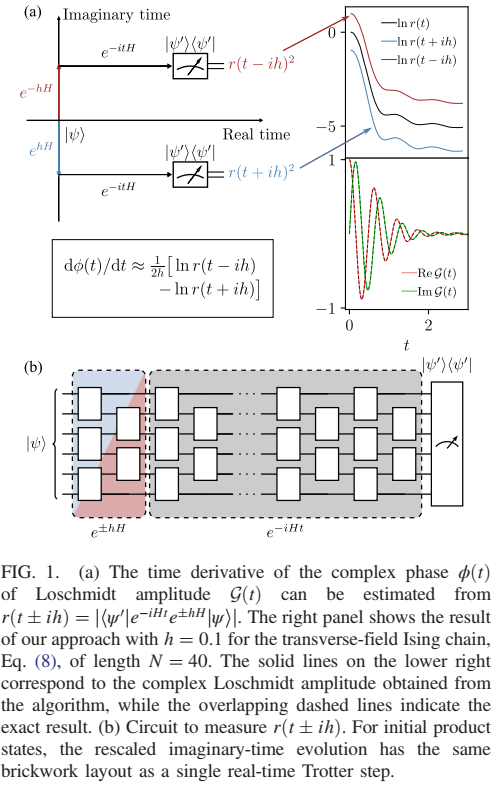
Hadamard test, give rise to large overheads due to the need for global controlled-unitary operations. We introduce a quantum algorithm based on complex
analysis that overcomes this problem for amplitudes that are a continuous function of time. Our method only requires the implementation of real-time evolution
and a shallow circuit that approximates a short imaginary-time evolution. We show that the method outperforms the Hadamard test in terms of circuit depth
and that it is suitable for current noisy quantum computers when combined with a simple error-mitigation strategy.

Article: https://doi.org/10.1103/PhysRevLett.132.220601
