A logical qubit-design with geometrically tunable error-resistibility

    Breaking the error-threshold would mark a milestone in establishing quantum advantage for a wide range of relevant problems. One possible route is to encode information redundantly in a logical qubit by combining several noisy qubits, providing an increased robustness against external perturbations. We propose a setup for a logical qubit built from superconducting qubits (SCQs) coupled to a microwave cavity-mode. Our design is based on a recently discovered geometric stabilizing mechanism in the Bose-Hubbard wheel (BHW), which manifests as energetically well-separated clusters of many-body eigenstates. We investigate the impact of experimentally relevant perturbations between SCQs and the cavity on the spectral properties of the BHW. We show that even in the presence of typical fabrication uncertainties, the occurrence and separation of clustered many-body eigenstates is extremely robust. Introducing an additional, frequency-detuned SCQ coupled to the cavity yields duplicates of these clusters, that can be split up by an on-site potential. We show that this allows to (i) redundantly encode two logical qubit states that can be switched and read out efficiently and (ii) can be separated from the remaining many-body spectrum via geometric stabilization. We demonstrate at the example of an X-gate that the proposed logical qubit reaches single qubit-gate fidelities > 0.999 in experimentally feasible temperature regimes ∼ 10−20 mK.

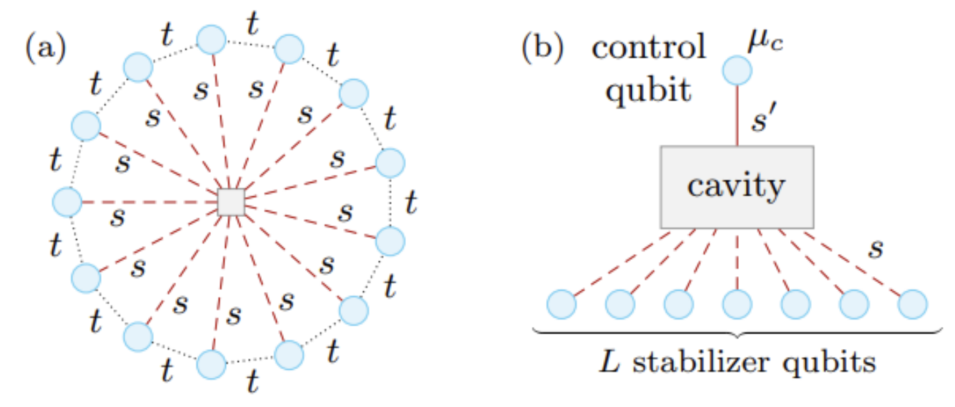
Lattice geometry of the Bose-Hubbard wheel

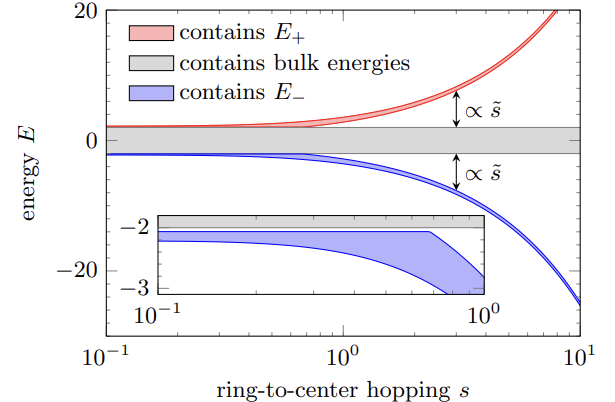
Established bounds for the single-particle spectrumof the perturbed BHW.

CONCLUSION:

We proposed a logical qubit construction scheme based on the peculiar property of the BHW (in the infinitite U limit) to open a gap between clusters of many-body eigenstates with the energetically lowest states exhibiting Bose-Einstein condensation. Exploiting the fact that this gap scales ∝√L where L is the number of lattice sites on the outer ring, i.e., the coordination number, we suggest a setup for the logical qubit in which these hard core-bosonic sites are realized by SC stabilizer qubits, and the all-to-one coupling to the wheel’s center site is implemented by resonantly coupling the qubits to a cavity mode. This way, the energetically low-lying cluster of many-body eigenstates of the BHW can be separated from the remaining part of the spectrum by increasing the number of stabilizer qubits. For the resulting architecture, we investigated the robusteness of the separation of this cluster in the presence of disorder to evaluate the effect of experimental imperfections. We derived bounds on the induced perturbations under the assumption that the couplings between the qubits and the cavity mode are subject to normal distributed imperfections and showed that corrections to the gap-opening are occurring only in second order in the standard deviation σ. Taking into account the robustness of the BHW against local perturbation on the outer ring (the stabilizer qubits), we expect the logical qubit setup to be remarkably stable against fabrication errors. 

Article：arXiv:2405.08138v1