A complexity efficient penta-diagonal quantum smoothing filter for bio-medical signal denoising: a study on ECG
1143 浏览Extracting information‑bearing signalfrom a noisy environment has been a practical challenge in both classical andquantum computing formalism, especially in critical signal processingapplications. To filter out the effect of noise, we propose a quantum smoothingfilter built upon quantum formalism‑based circuits applied forelectrocardiogram signal denoising. The proposed quantum filter is a conceptuallynovel framework with an advantage in computational complexity as compared tothe existing classical filters, such asdiscrete wavelet transform and empirical mode decomposition, whereas itachieves similar performance metrics for the accuracy of the filter. Further,we exploit the penta‑diagonal Toeplitz structure of the smoothing filter, whichgives approximately 48% gate cost reduction for 10 qubit circuit compared tothe standard Hamiltonian simulation without structure. The run‑time complexityusing the quantum matrix inversion technique for the structured matrix is givenby ![]() for condition number κof the N × N filter matrix within precision εP. Embedding fixed sparsity of thebanded matrix, the quantum filter shows potentially better run‑time complexity thanclassical filtering techniques. For the quantifiable research results of ourwork, we have shown several performance metrics, such as mean‑square error andpeak signal‑to‑noise ratio analysis, with a bound of error due to observationnoise, simulation error and quantum measurement uncertainty.
for condition number κof the N × N filter matrix within precision εP. Embedding fixed sparsity of thebanded matrix, the quantum filter shows potentially better run‑time complexity thanclassical filtering techniques. For the quantifiable research results of ourwork, we have shown several performance metrics, such as mean‑square error andpeak signal‑to‑noise ratio analysis, with a bound of error due to observationnoise, simulation error and quantum measurement uncertainty.
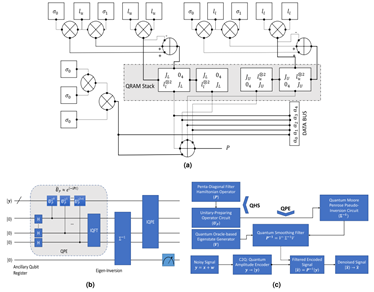
Figure1. Quantum architecture and flow-diagram for signal denoising. (a) The proposedquantum architecture for a penta-diagonal banded Toeplitz Hamiltonian of size8×8 using elementary quantum gates: Here, dark dots represent connections, thecircle ⊗ notation represents tensor operation, circle ⊕ represents the adder circuit, σ0,σ1,lu, ll , JU, JL are identity gate, Pauli-x operator, upper-ladder, and lower-ladderoperator, upper-Jordan gate, and lower-Jordan gates respectively, a0, . . . ,a4are the filter coefficients with a1 = a3, a2 = a4, and QRAM represents quantumrandom access memory. (b) A quantum circuit of a quantum filter using thequantum phase estimation circuit using the proposed quantum filter: thesub-system in as shown in (a) is used here as controlled unitaryUP
Reference:https://www.nature.com/articles/s41598-024-59851-5
