Passive error correction with a qubit-oscillator system in noisy environment
2769 浏览https://arxiv.org/pdf/2408.05145
In this paper, we study an open quantum system consisting of a qubit coupled to a harmonic oscillator subject to two-photon relaxation and demonstrate that such a system can be utilized to construct a cat qubit capable of passive error correction. To this end, we first show that the steady state of the qubit-oscillator system, described by the open quantum Rabi model with two-photon relaxation, undergoes a superradiant phase transition that breaks the strong symmetry of the Lindblad master equation. In the strong symmetry-broken phase, we show that a cat qubit can be stabilized in the steady state by tuning the qubit-oscillator coupling strength and demonstrate that passive error correction can be realized against errors due to fluctuations in the system frequencies. Our study deepens the understanding of dissipative phases in a qubit-oscillator system with strong symmetry and paves the way to utilize them for passive error correction.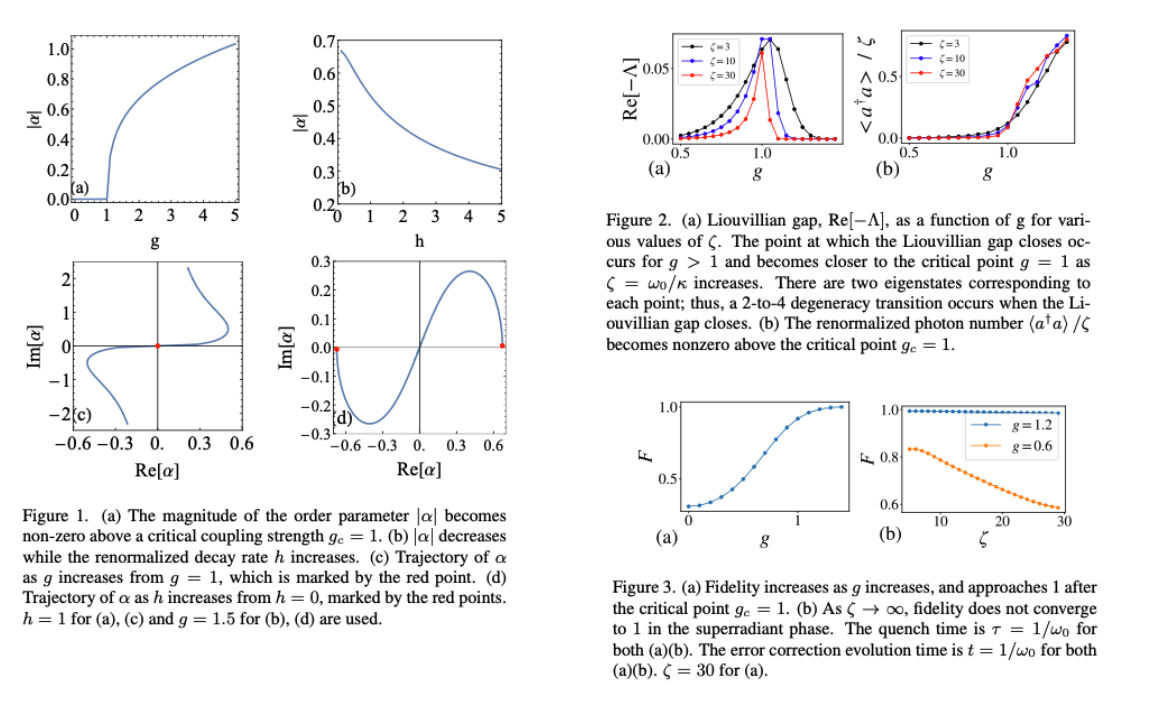
In this paper, we have studied the open quantum Rabi model with two-photon relaxation as a minimal model that under- goes a SPT, spontaneously breaking a strong parity symmetry. We have demonstrated that the closing Liouvillian gap and the quadruply degenerate steady-states emerge in the superradi- ant phase. Moreover, our proposal for a passive error correc- tion based on a strong symmetry-breaking SPT paves the way to realize a stabilized bosonic cat code by utilizing a qubit- oscillator coupling, distinct from previous proposals based on parametric two-photon driving and Kerr nonlinear-ity . Given that the mean-field equations of motion for the open Dicke model with two-photon relaxation, which realizes a conventional thermodynamic limit with an infinite number of qubits, can be made identical to the current model after proper renormalization, we anticipate that the prop- erties and applications of the phase transition we discovered for a single oscillator-qubit system can be generalized to an oscillator coupled to an ensemble of qubits, making our study relevant for a wide range of quantum systems.
