Tensor-based quantum phase difference estimation for large-scale demonstration
2791 浏览https://arxiv.org/pdf/2408.04946v1
We develop an energy calculation algorithm leveraging quantum phase dif- ference estimation (QPDE) scheme and a tensor-network-based unitary com- pression method in the preparation of superposition states and time-evolution gates. Alongside its efficient implementation, this algorithm reduces depolar- ization noise affections exponentially. We demonstrated energy gap calcula- tions for one-dimensional Hubbard models on IBM superconducting devices using circuits up to 32-system (plus one-ancilla) qubits, a five-fold increase over previous QPE demonstrations, at the 7242 controlled-Z gate level of stan- dard transpilation, keying a Q-CTRL error suppression module. Additionally, we propose a technique towards molecular executions using spatial orbital localization and index sorting, verified by an eight-qubit butadiene simulation. Since QPDE can handle the same objectives as QPE, our algorithm represents a leap forward in quantum computing on real devices.
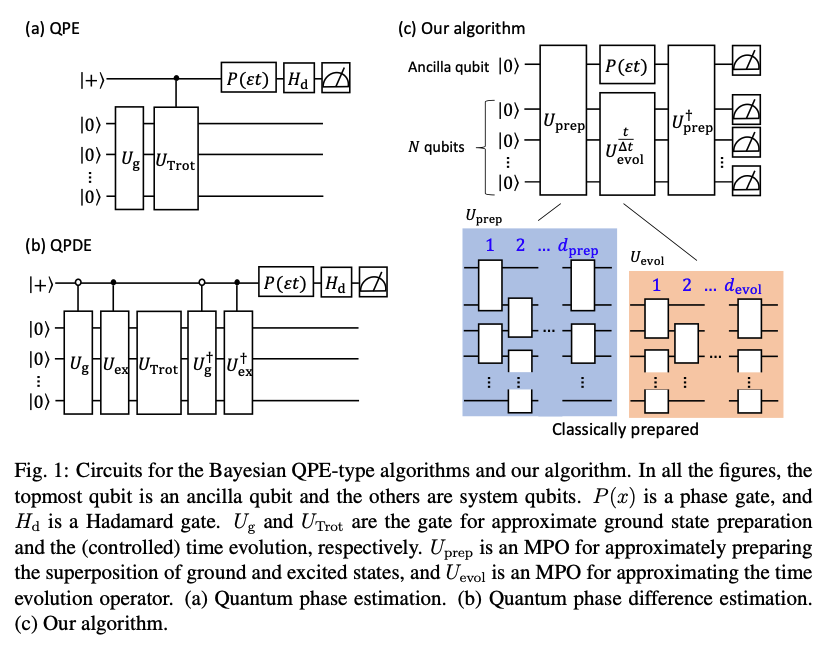
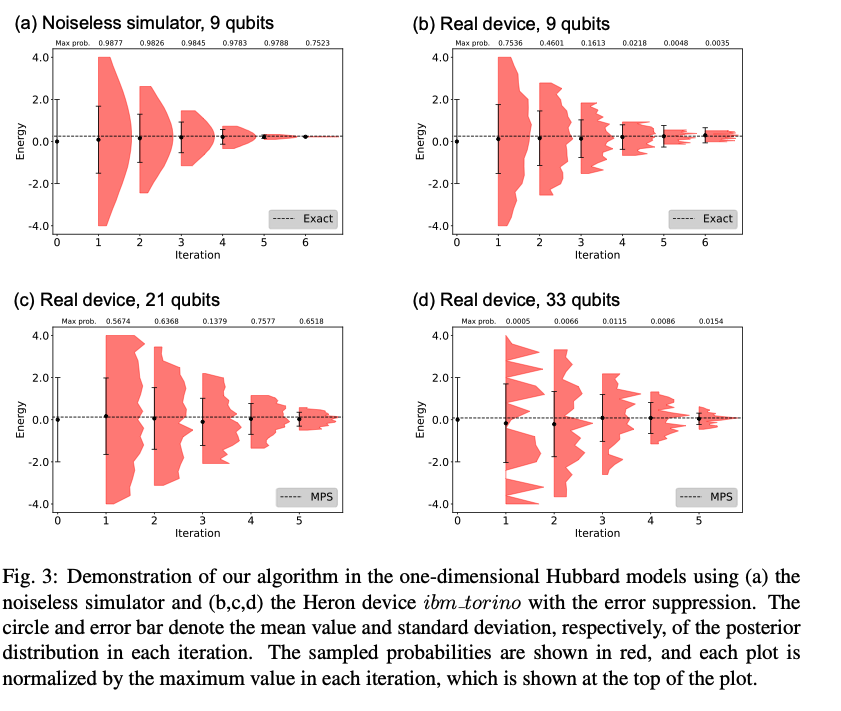
We have proposed a gate-efficient and noise-robust quantum phase estimation-type algorithm based on unitary compression by tensor networks. We applied the algorithm to a one-dimensional Hubbard model and confirmed its effectiveness on a real superconducting device, utilizing an error suppression module, with circuits up to 33 qubits including one ancilla qubit. Further- more, for the calculation of chemical models, we proposed a procedure to convert the model composed of molecular orbitals into a one-dimensional model by orbital localization and re- ordering, achieving over 40% improvement in the error metric. These results enable large-scale implementations of quantum phase estimation-type algorithms.
The most significant challenge is an improvement of estimation to achieve chemical ac- curacy. A deeper MPO improves accuracy, but in general, the computational cost increases exponentially with depth. Since our unitary compression can be extended to tensor networks other than MPO, tensor networks that account for non-linearity in device connectivity — for example heavy hex on IBM devices or two-dimensional grids on Google devices (38). In the case of ion- or atom-trapped hardware, physical constraints on the transport of the parti- cles would influence the optimal tensor structure for the algorithm. Alternatively, integrating quantum-classical hybrid-optimized circuit to Uprep can improve accuracy .
Finally, in addition to QPE forming the basis of quantum computation, the technique we proposed for superposition state preparation to avoid long-range interactions involving an an- cilla qubit can be used for more general circuit compilation. Hence, the proposed algo- rithms or techniques have potential applications in other fields besides chemistry, such as the Harrow–Hassidim–Lloyd algorithm in machine learning.
