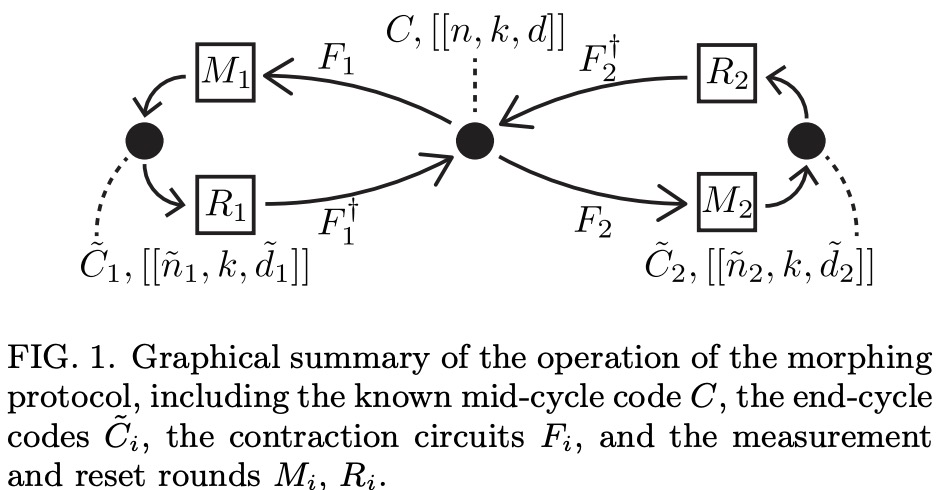
Lowering Connectivity Requirements For Bivariate Bicycle Codes Using Morphing Circuits

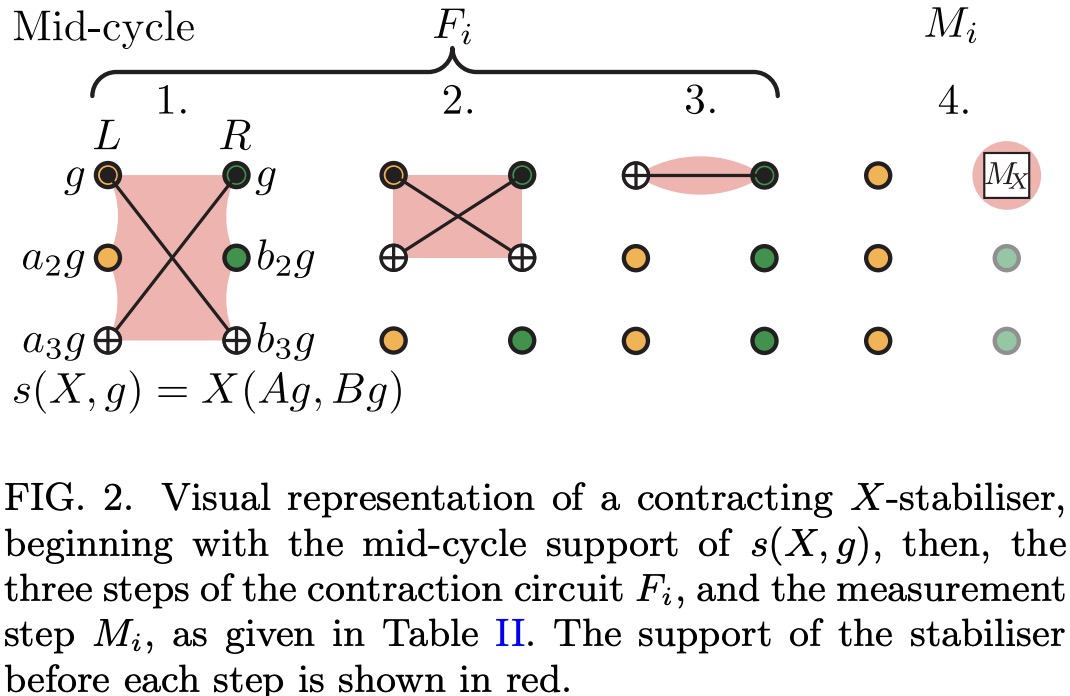
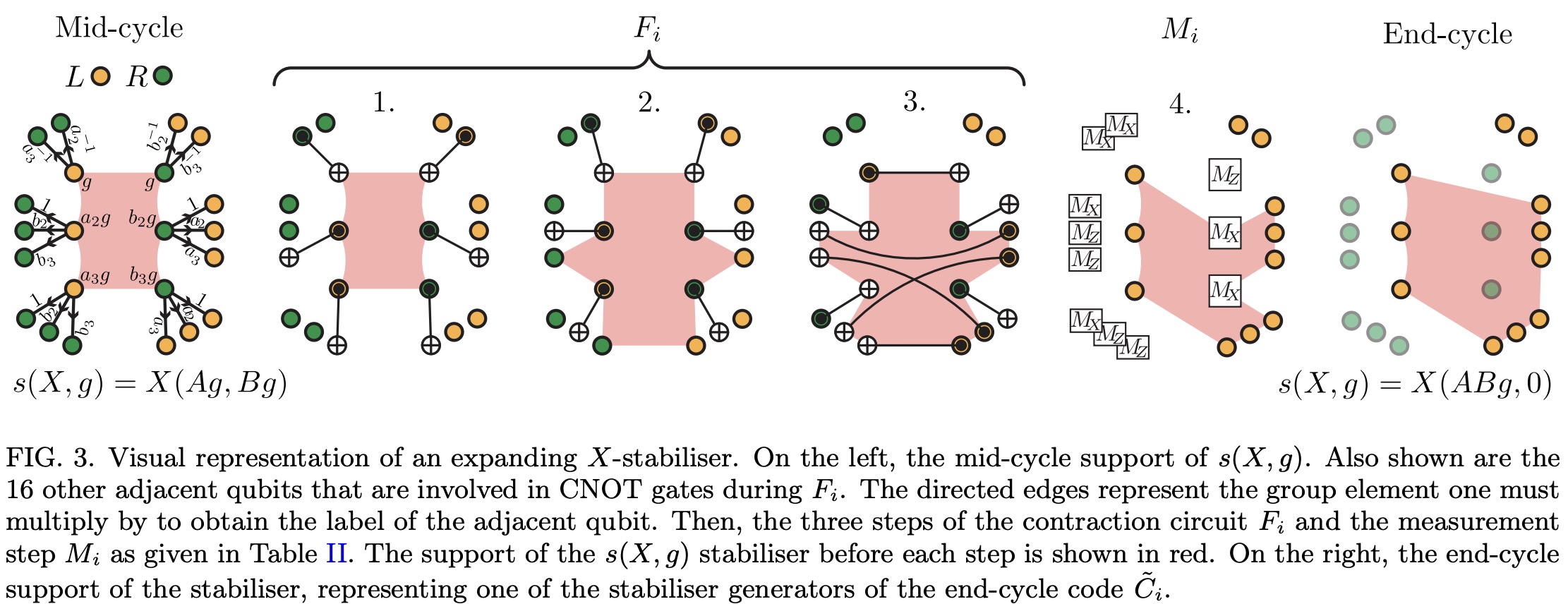
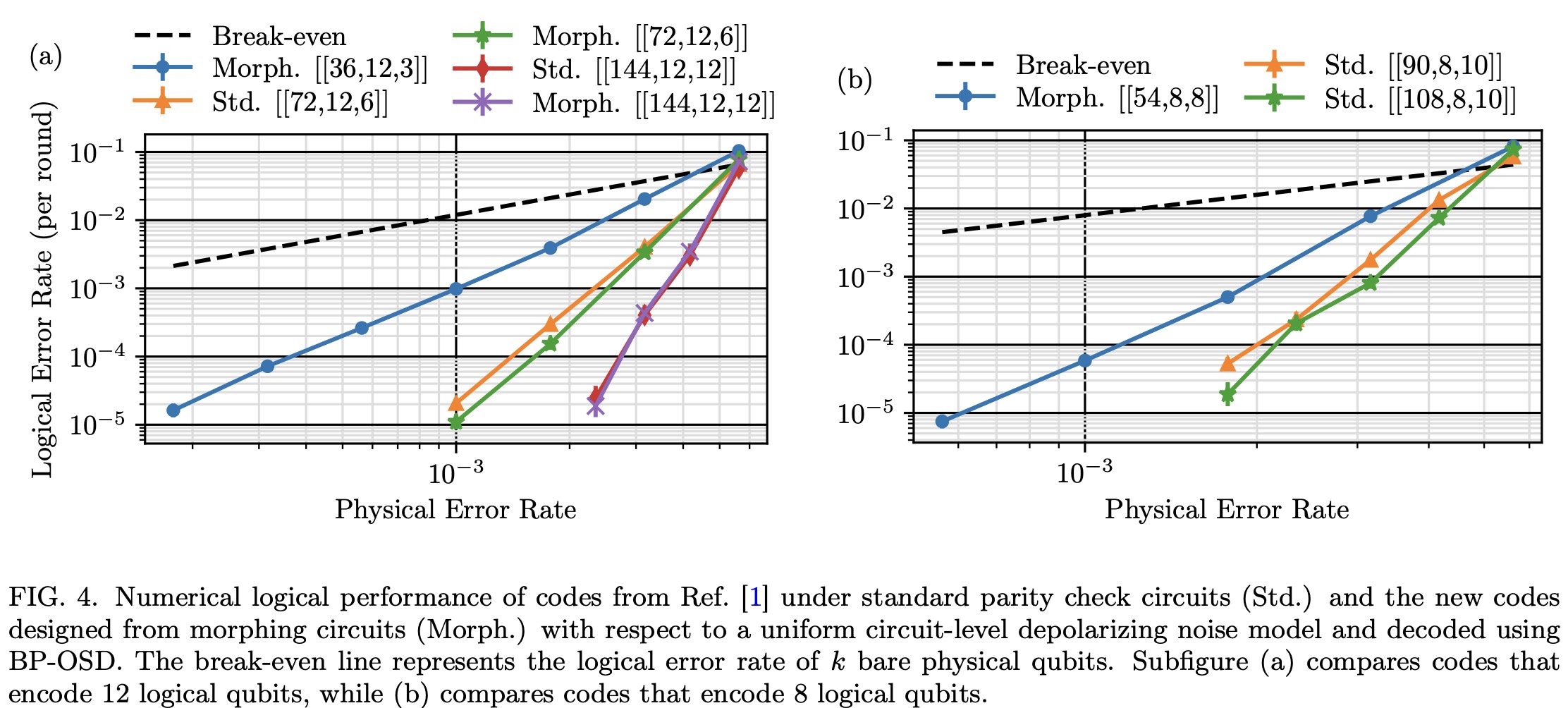
Recently, Bravyi et al. [1] proposed a set of small quantum Bivariate Bicycle (BB) codes that achieve a similar circuit-level error rate to the surface code but with an improved encoding rate. In this work, we generalise a novel parity-check circuit design principle that we call morphing circuits (first introduced in [2]) and apply this methodology to BB codes. Our construction generates a new family of BB codes — including a new [[144, 12, 12]] “gross” code — whose parity check circuits require a qubit connectivity of degree five instead of six. Intriguingly, each parity check circuit requires only 6 rounds of CNOT gates — one fewer than in Ref. [1] — even though our new codes have weight-9 stabilisers. We also show how to perform logical input/output circuits to an ancillary rotated surface code using morphing circuits, all within a biplanar layout. The new codes perform at least as well as those of Ref. [1] under uniform circuit-level noise when decoded using BP-OSD. Finally, we develop a general framework for designing morphing circuits and present a sufficient condition for its applicability to two-block group algebra codes.