Towards Adiabatic Quantum Computing Using Compressed Quantum Circuits
2024-06-14 18:32
1084 浏览
We describe tensor network algorithms to optimize quantum circuits for adiabatic quantum computing. To suppress diabatic transitions, we include counterdiabatic driving in the optimization and utilize
variational matrix product operators to represent adiabatic gauge potentials. Traditionally, Trotter product
formulas are used to turn adiabatic time evolution into quantum circuits and the addition of counterdiabatic driving increases the circuit depth per time step. Instead, we classically optimize a parameterized
quantum circuit of fixed depth to simultaneously capture adiabatic evolution together with counterdiabatic
driving over many time steps. The methods are applied to the ground-state preparation of quantum Ising
chains with transverse and longitudinal fields. We show that the classically optimized circuits can significantly outperform Trotter product formulas. Additionally, we discuss how the approach can be used for
combinatorial optimization.
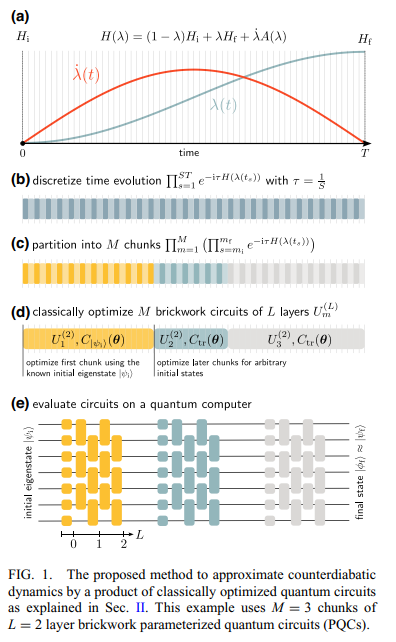
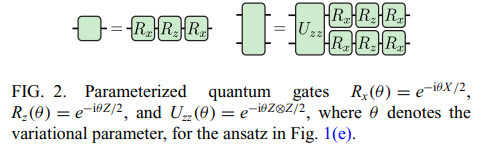


Article: https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.5.020362
