Quantum optimization using a 127-qubit gate-model IBM quantum computer can outperform quantum annealers for nontrivial binary optimization problems

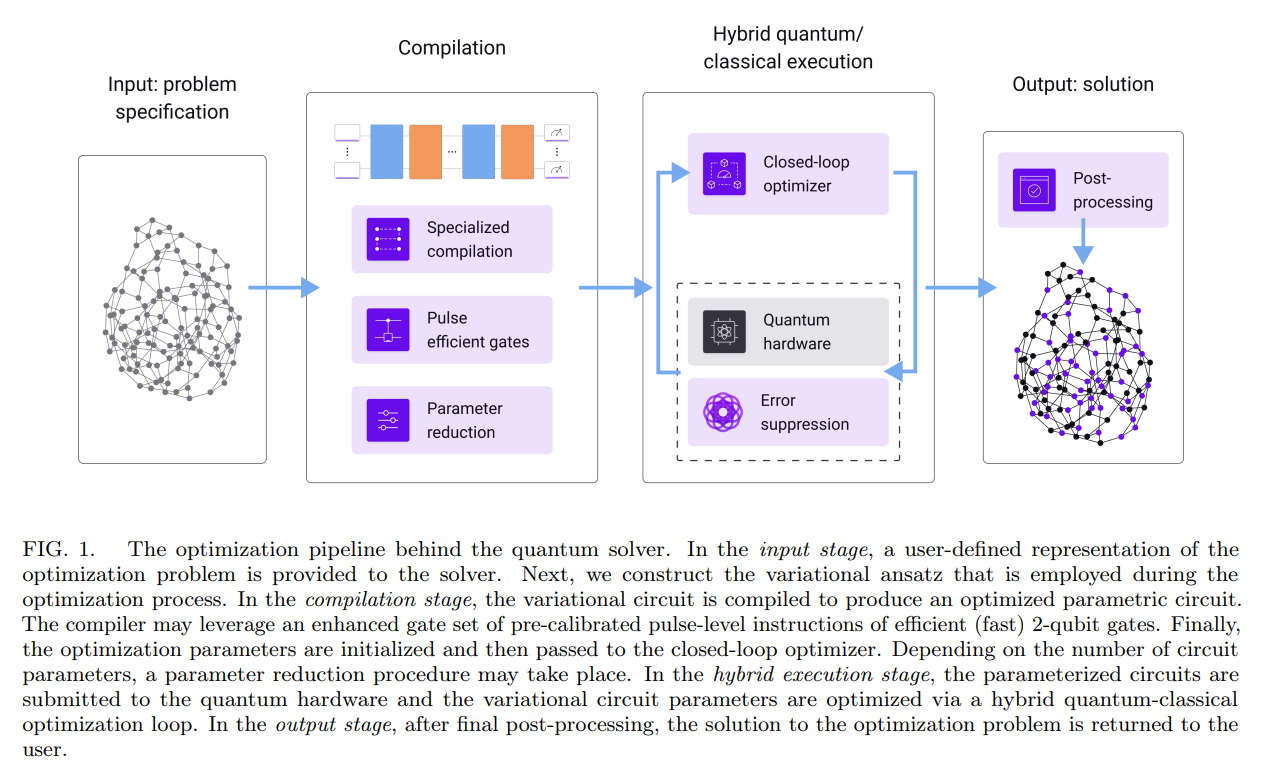
  We introduce a comprehensive quantum solver for binary combinatorial optimization problems on gate-model quantum computers that outperforms any published alternative and consistently delivers correct solutions for problems with up to 127 qubits. We provide an overview of the internal workflow, describing the integration of a customized ansatz and variational parameter update strategy, efficient error suppression in hardware execution, and overhead-free post-processing to correct for bit-flip errors. We benchmark this solver on IBM quantum computers for several classically nontrivial unconstrained binary optimization problems—the entire optimization is conducted on hardware with no use of classical simulation or prior knowledge of the solution. First, we demonstrate the ability to correctly solve Max-Cut instances for random regular graphs with a variety of densities using up to 120 qubits, where the graph topologies are not matched to device connectivity. These demonstrations are at least 4× larger than previous successful implementations on a trapped-ion quantum computer and deliver up to 9× increased likelihood of success for identical problem instances at the scale of 32 qubits. Next, we apply the solver to higher-order binary optimization and successfully search for the ground state energy of a 127-qubit spin-glass model with linear, quadratic, and cubic interaction terms. Use of this new quantum solver increases the likelihood of finding the minimum energy by up to ∼ 1, 500× relative to published results using a DWave annealer, and it can find the correct solution when the annealer fails. Furthermore, for both problem types, the Q-CTRL solver outperforms a heuristic local solver used to indicate the relative difficulty of the problems pursued. Overall, these results represent the largest quantum optimizations successfully solved on hardware to date, and demonstrate the first time a gate-model quantum computer has been able to outperform an annealer for a class of binary optimization problems.

Article:  https://arxiv.org/abs/2406.01743