Flux-charge symmetric theory of superconducting circuits
2024-05-29 09:31
1433 浏览
The quantum mechanics of superconducting circuits is derived by starting from a classical Hamiltonian dynamical system describing a dissipationless circuit,
usually made of capacitive and inductive elements. However, standard approaches to circuit quantization treat fluxes and charges, which end up as the canonically
conjugate degrees of freedom on phase space, asymmetrically. By combining intuition from topological graph theory with a recent symplectic geometry approach
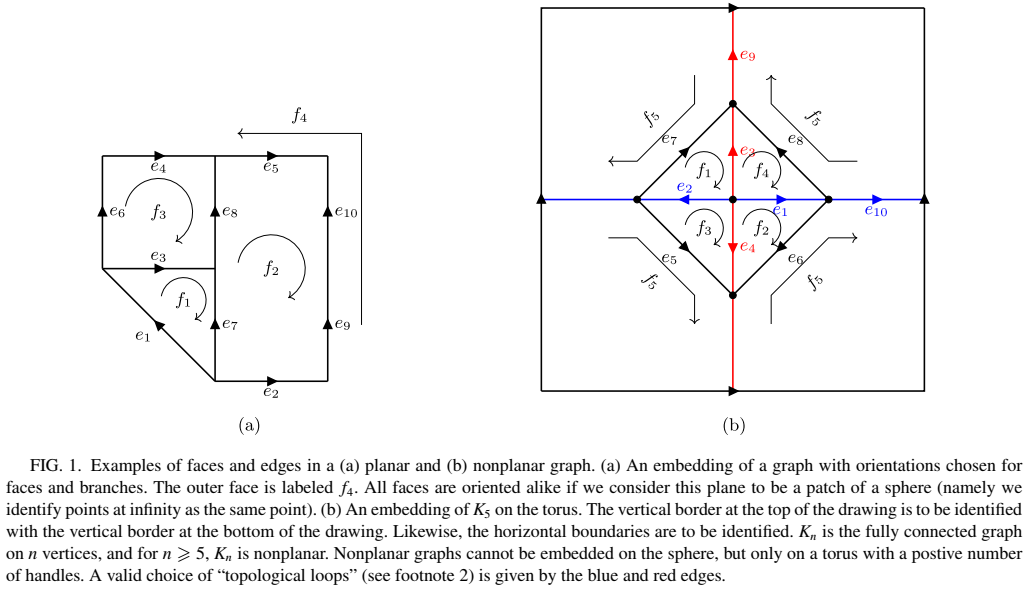
to circuit quantization, we present a theory of circuit quantization that treats charges and fluxes on a manifestly symmetric footing. For planar circuits, known
circuit dualities are a natural canonical transformation on the classical phase space. We discuss the extent to which such circuit dualities generalize to nonplanar
circuits.

Article:https://doi.org/10.1103/PhysRevB.109.174524
