Automated Synthesis of Fault-Tolerant State Preparation Circuits for Quantum Error Correction Codes

2024-08-23 10:17　68 浏览

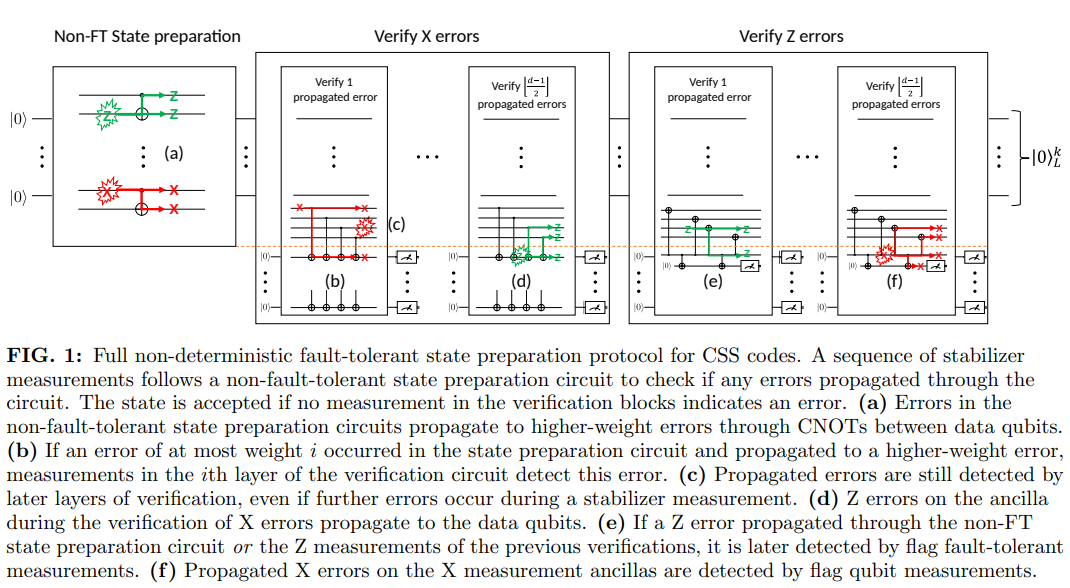
A central ingredient in fault-tolerant quantum algorithms is the initialization of a logical state for a given quantum error-correcting code from a set of noisy qubits. A scheme that has demonstrated promising results for small code instances that are realizable on currently available hardware composes a non-fault-tolerant state preparation step with a verification step that checks for spreading errors. Known circuit constructions of this scheme are mostly obtained manually, and no algorithmic techniques for constructing depth- or gate-optimal circuits exist. As a consequence, the current state of the art exploits this scheme only for specific code instances and mostly for the special case of distance 3 codes. In this work, we propose an automated approach for synthesizing fault-tolerant state preparation circuits for arbitrary CSS codes. We utilize methods based on satisfiability solving (SAT) techniques to construct fault-tolerant state preparation circuits consisting of depth- and gate-optimal preparation and verification circuits. 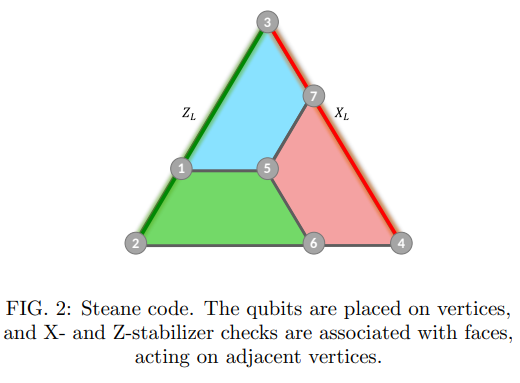We also provide heuristics that can synthesize fault-tolerant state preparation circuits for code instances where no optimal solution can be obtained in an adequate timeframe. Moreover, we give a general construction for nondeterministic state preparation circuits beyond distance 3. Numerical evaluations using d = 3 and d = 5 codes confirm that the generated circuits exhibit the desired scaling of the logical error rates. The resulting methods are publicly available as part of the Munich Quantum Toolkit (MQT) at https://github.com/cda-tum/mqt-qecc. Such methods are an important step in providing faulttolerant circuit constructions that can aid in near-term demonstration of fault-tolerant quantum computing.