Optimal number of stabilizer measurement rounds in an idling surface code patch
2782 浏览https://arxiv.org/abs/2408.07529
Logical qubits can be protected against environmental noise by encoding them into a highly entangled state of many physical qubits and actively intervening in the dynamics with stabilizer measurements. In this work, we numerically optimize the rate of these interventions: the number of stabilizer measurement rounds for a logical qubit encoded in a surface code patch and idling for a given time. We model the environmental noise on the circuit level, including gate errors, readout errors, amplitude and phase damping. We find, qualitatively, that the optimal number of stabilizer measurement rounds is getting smaller for better qubits and getting larger for better gates or larger code sizes. We discuss the implications of our results to some of the leading architectures, superconducting qubits, and neutral atoms.
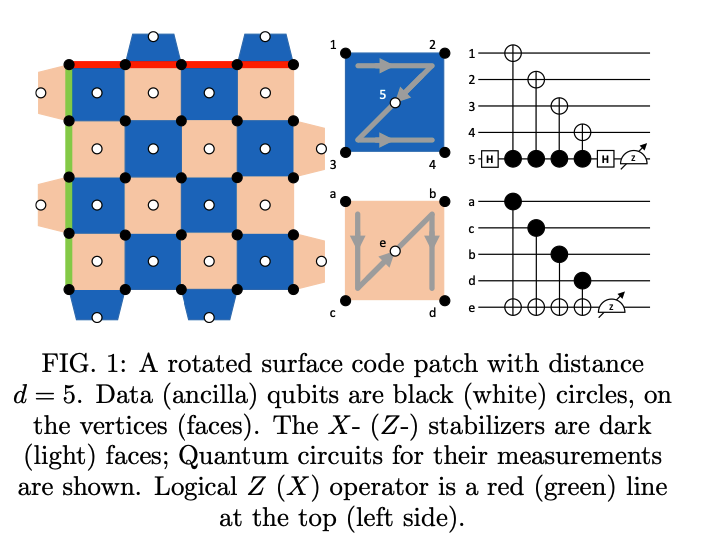
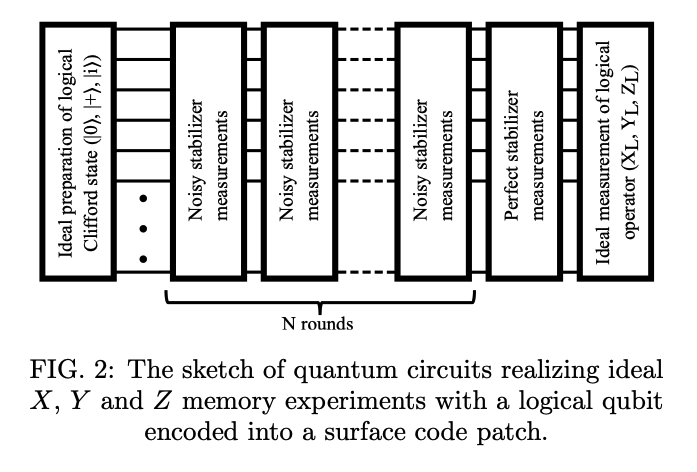
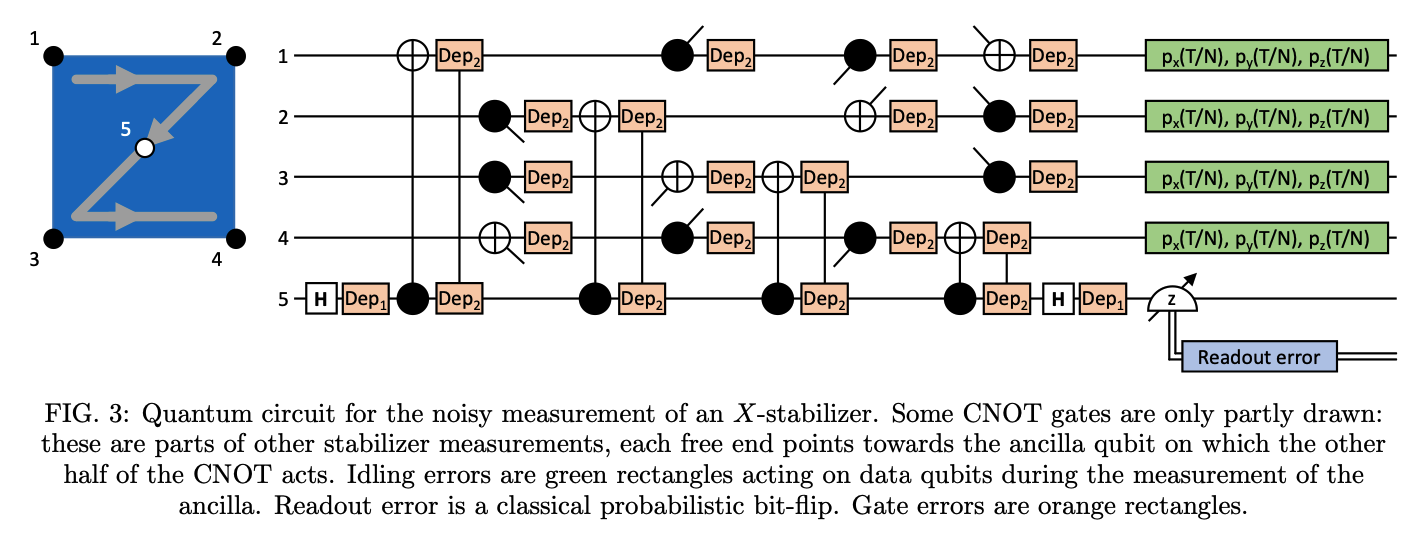
In this work we numerically characterized the logical noise channel of an idling surface code patch across var- ious code distances, number of stabilizer measurement rounds, and noise parameters. For each set of noise parameters and code distances, we determined an opti- mal number for stabilizer measurement rounds, N∗, that maximizes the performance of the surface code patch dur- ing a fixed idling time. Our circuit-level noise model incorporated both time-dependent dynamic errors, am- plitude and phase damping of data qubits, and time- independent static gate and readout errors.
Our results indicate that N∗ decreases with higher qubit quality, while it increases with higher gate qual- ity and larger code sizes. We also explored the ap- plicability of our findings to superconducting and neu- tral atom devices, revealing distinct optimal strategies for these two architectures. Specifically, for supercon- ducting qubits, the optimal strategy involves performing the maximum feasible number of stabilizer measurement rounds, whereas for neutral atoms, the optimal number is significantly lower than the maximum feasible.
Including more sophisticated errors, such as leakage [32], crosstalk [36, 37], or correlated errors [35] would be an interesting extension of our work, as would consid- ering more parameters to optimize on (e.g., code, code distance, reset after measurements) to get the best per- formance, as in [42, 43].
We believe our results will be valuable for instrumen- talists aiming to further optimize the performances of log- ical qubits encoded into quantum error-correcting codes.
