Topological quantum compilation of two-qubit gates
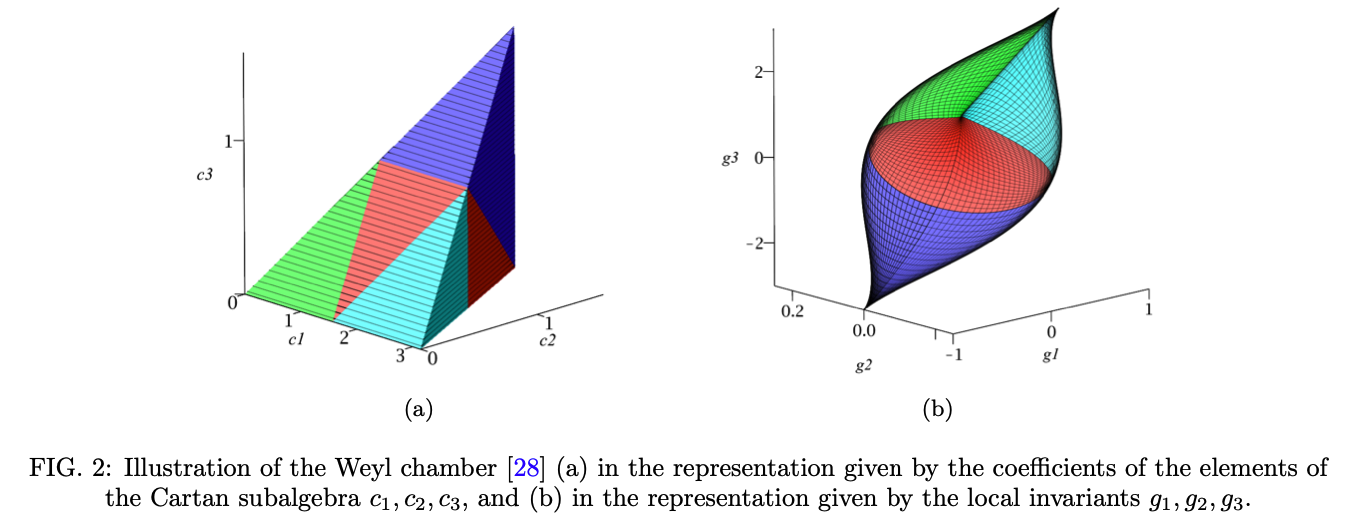
2838 浏览We investigate the topological quantum compilation of two-qubit operations within a system of Fibonacci anyons. Our primary goal is to generate gates that are approximately leakage-free and equivalent to the controlled-NOT (CNOT) gate up to single-qubit operations. These gates belong to the local equivalence class [CNOT]. Additionally, we explore which local equivalence classes of two-qubit operations can be naturally generated by braiding Fibonacci anyons. We discovered that most of the generated classes are located near the edges of the Weyl chamber representation of two-qubit gates, specifically between the local equivalence classes of the identity and [CNOT], and between those of the double-controlled-NOT [DCNOT] and [SWAP]. Furthermore, we found a numerically exact implementation of a local equivalent of the SWAP gate using a sequence of only nine elements from the Fibonacci braiding gate set.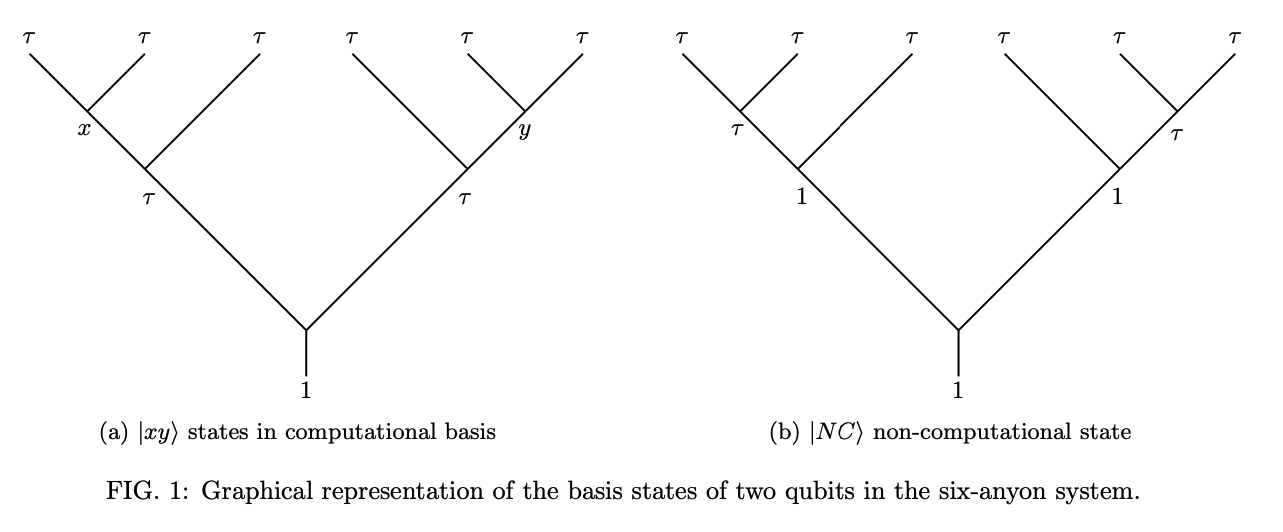
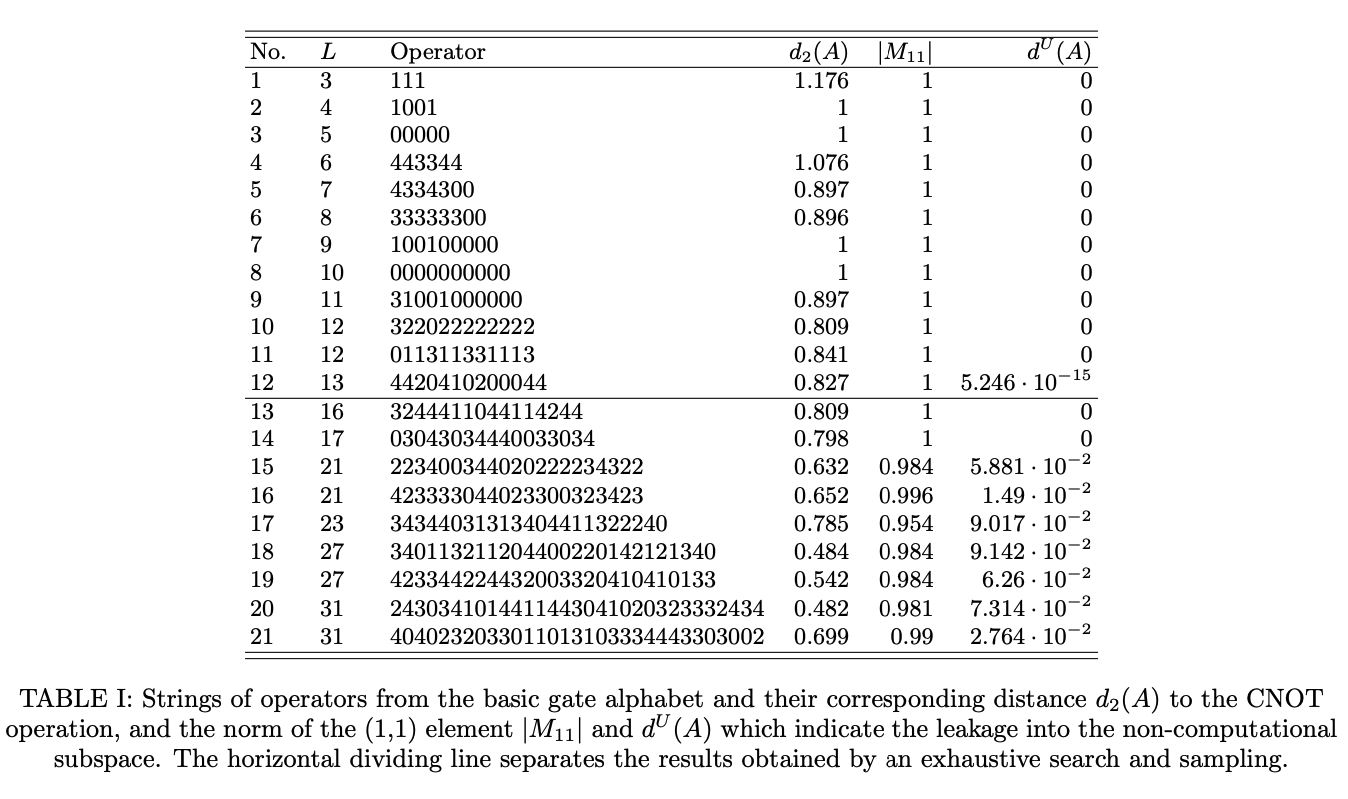
We numerically address the problem of topological compilation of two-qubit operations in the system of six Fibonacci anyons. This system gives rise to a five-dimensional Hilbert space which permits encoding of two qubits while leaving one-dimensional subspace as non-computational. This encoding has previously been studied by Cui et al. [23] who focused on the question of leakage-free two-qubit operations that are at the same time also entangling. They performed brute-force numerical searches for anyon braids with a length up to seven but found no entangling gates that would be exactly leakage-free.
