Linear-Size Ancilla Systems for Logical Measurements in QLDPC Codes

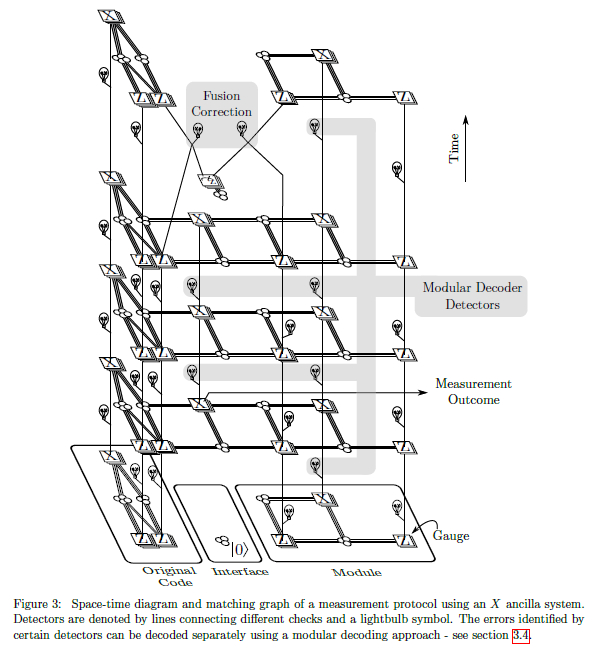
We show how to perform all logical Clifford gates on the [[144,12,12]] bivariate bicycle code, also known as the gross code. The scheme adds about 100 ancilla qubits into the connectivity graph, and one of the twelve logical qubits is sacrificed for gate synthesis. Logical measurements are combined with the automorphism gates studied by Bravyi et al. (Nature 627, 778-782) to implement 288 Pauli product measurements. We demonstrate the practicality of our scheme through circuit-level noise simulations, leveraging a novel modular decoder that combines BPOSD with matching. The main technical contribution is a lower overhead logical measurement scheme based on gauge-fixing the construction by Cohen et al. (Sci. Adv. 8, eabn1717). Our techniques apply to general CSS codes and leverage expansion properties of the Tanner graph to give rigorous guarantees on qubit count, code distance, fault distance, and decoding distance of the modular decoder. In particular, we require O(d/β) additional qubits where β is the boundary Cheeger constant of the subgraph supporting the logical operator being measured. By introducing O(d) additional bridge qubits, we are also able to measure products of logical Pauli operators and logical Y operators.

https://arxiv.org/abs/2407.18393