Advantage of Quantum Neural Networks as Quantum Information Decoders

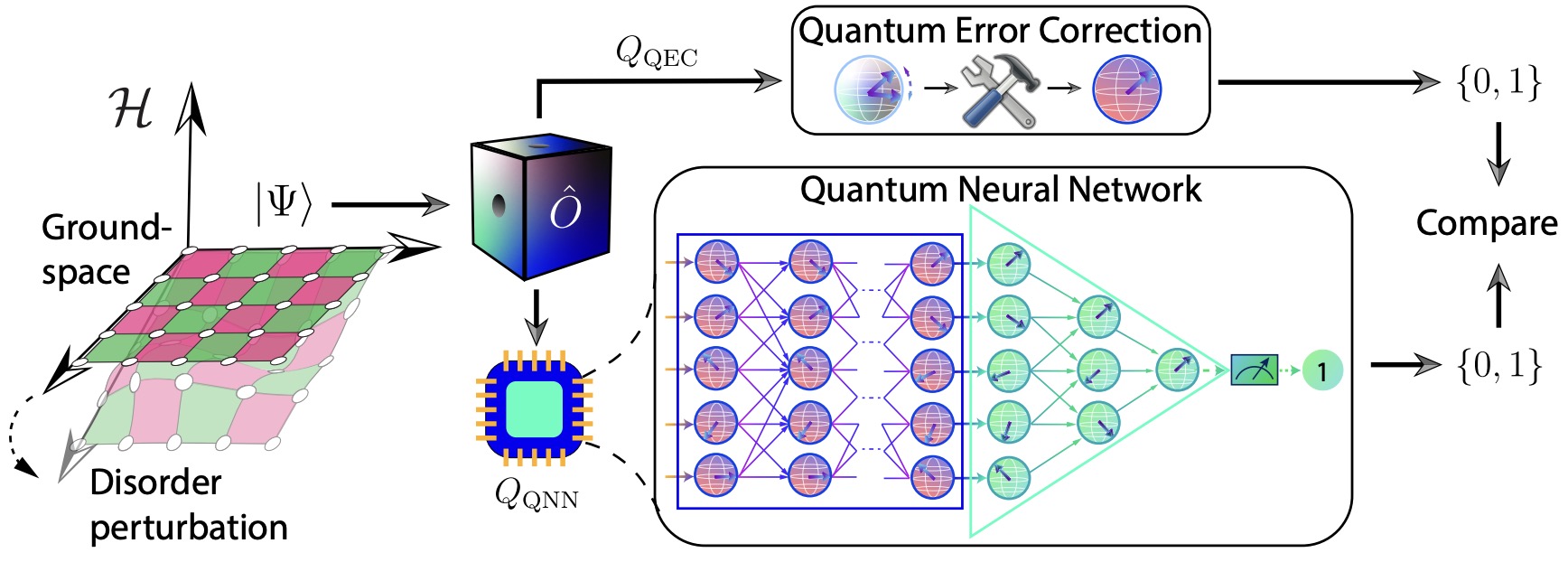
A promising strategy to protect quantum information from noise-induced errors is to encode it into the low-energy states of a topological quantum memory device. However, readout errors from such memory under realistic settings is less understood. We study the problem of decoding quantum information encoded in the groundspaces of topological stabilizer Hamiltonians in the presence of generic perturbations, such as quenched disorder. 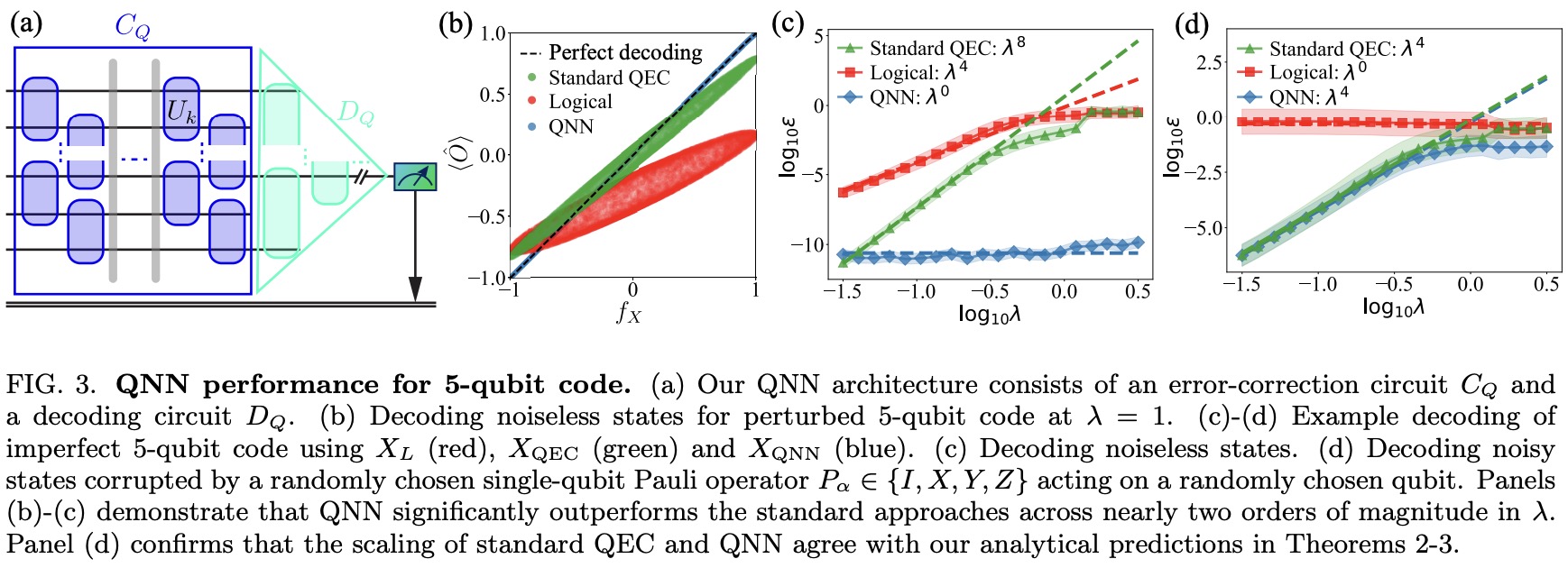We first prove that the standard stabilizerbased error correction and decoding schemes work adequately well in such perturbed quantum codes by showing that the decoding error diminishes exponentially in the distance of the underlying unperturbed code. We then prove that Quantum Neural Network (QNN) decoders provide an almost quadratic improvement on the readout error. Thus, we demonstrate provable advantage of using QNNs for decoding realistic quantum error-correcting codes, and our result enables the exploration of a wider range of non-stabilizer codes in the near-term laboratory settings.