Agnostic Phase Estimation

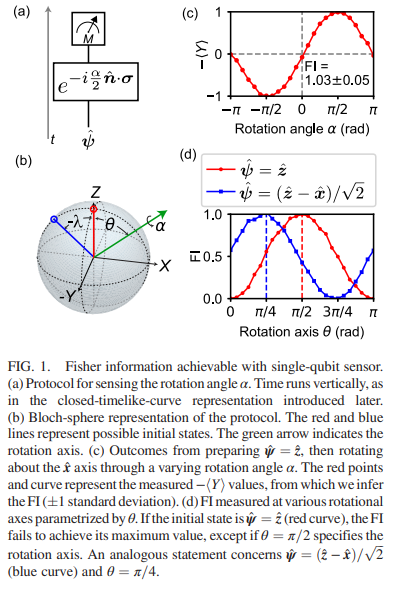
    The goal of quantum metrology is to improve measurements’ sensitivities by harnessing quantum resources. Metrologists often aim to maximize the quantum Fisher information, which bounds the measurement setup’s sensitivity. In studies of fundamental limits on metrology, a paradigmatic setup features a qubit (spin-half system) subject to an unknown rotation. One obtains the maximal quantum Fisher information about the rotation if the spin begins in a state that maximizes the variance of the rotationinducing operator. If the rotation axis is unknown, however, no optimal single-qubit sensor can be prepared. 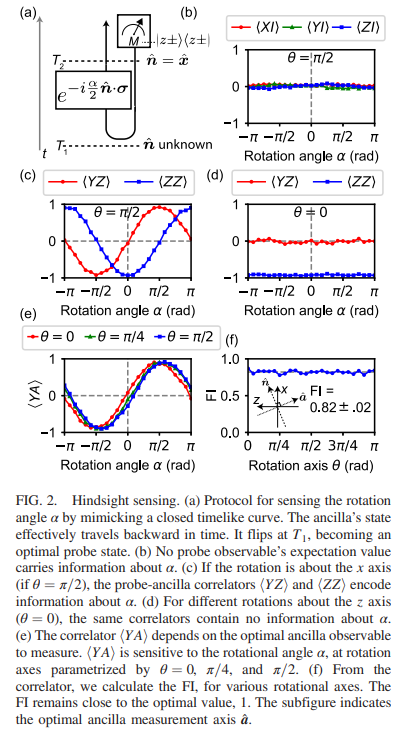Inspired by simulations of closed timelike curves, we circumvent this limitation. We obtain the maximum quantum Fisher information about a rotation angle, regardless of the unknown rotation axis. To achieve this result, we initially entangle the probe qubit with an ancilla qubit. Then, we measure the pair in an entangled basis, obtaining more information about the rotation angle than any single-qubit sensor can achieve. 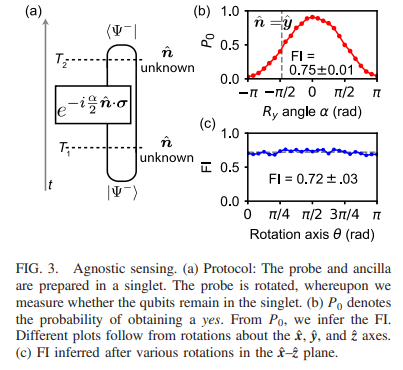We demonstrate this metrological advantage using a two-qubit superconducting quantum processor. Our measurement approach achieves a quantum advantage, outperforming every entanglement-free strategy.