Exploring quantum weight enumerators from the n-qubit parallelized SWAP test

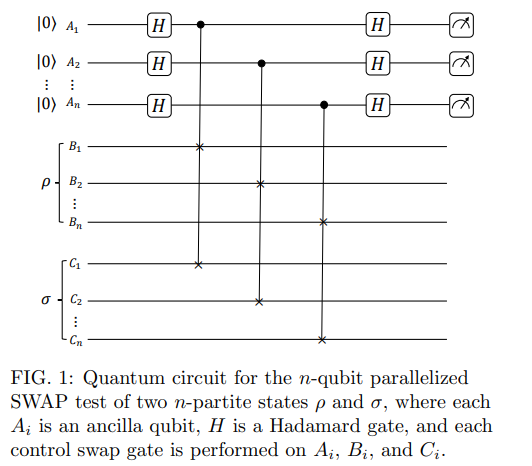
      Quantum weight enumerators play a crucial role in quantum error-correcting codes and multipartite entanglement. They can be used to investigate the existence of quantum error-correcting codes and k-uniform states. In this work, we build the connection between quantum weight enumerators and the n-qubit parallelized SWAP test. We discover that each shadow enumerator corresponds precisely to a probability in the n-qubit parallelized SWAP test, providing a computable and operational meaning for the shadow enumerators. Due to the non-negativity of probabilities, we obtain an elegant proof for the shadow inequalities. Concurrently, we can also calculate the Shor-Laflamme enumerators and the Rains unitary enumerators from the n-qubit parallelized SWAP test. For applications, we employ the n-qubit parallelized SWAP test to determine the distances of quantum error-correcting codes, and the k-uniformity of pure states. Our results indicate that quantum weight enumerators can be efficiently estimated on quantum computers, and opening a path to calculate the distances of quantum error-correcting codes.